Створення масивів рівномірно розподілених чисел з NumPy linspace()
У цьому керівництві ви ознайомитеся з використанням функції NumPy linspace() для генерації масивів із рівномірно розподіленими числовими значеннями в Python.
Ми розглянемо детальний синтаксис NumPy linspace() і продемонструємо його використання на конкретних прикладах.
Примітка: Для проходження цього навчального матеріалу необхідна наявність встановлених Python та NumPy.
Якщо ви ще не встановили NumPy, скористайтеся нашим коротким посібником з встановлення.
Почнімо!
Інсталяція та імпорт NumPy
Перед тим як перейти до основного матеріалу, розглянемо процес встановлення бібліотеки NumPy.
⏩ Якщо NumPy вже встановлено, ви можете пропустити цей розділ.
- Для використання Google Colab, хмарного середовища Jupyter, імпортуйте NumPy і одразу починайте кодувати (рекомендовано для цього керівництва ✅).
- Якщо ви віддаєте перевагу локальному середовищу, рекомендуємо встановити дистрибутив Anaconda Python. Він включає набір попередньо встановлених пакетів. Завантажте інсталятор для вашої операційної системи. Процес встановлення займе лише кілька хвилин. ⌛
- Якщо Python вже є на вашому комп’ютері, ви можете встановити Anaconda, щоб використовувати
condaабоpipдля встановлення та управління пакетами. Виконайте одну з наведених команд у командному рядку Anaconda:
# Встановлення NumPy за допомогою conda
conda install numpy
# Встановлення NumPy за допомогою pip
pip install numpy
Далі імпортуйте NumPy під псевдонімом np, використовуючи команду нижче. Це дозволить посилатися на NumPy через np замість повного імені модуля.
import numpy as np
В подальшому ми будемо використовувати точкову нотацію np.<назва-функції> для доступу до функцій бібліотеки NumPy.
Необхідність рівномірного розподілу чисел
Працюючи з масивами NumPy, часто виникає потреба у створенні масивів з рівномірно розподіленими числовими значеннями у визначеному діапазоні.
Перед тим, як рухатися далі, швидко розглянемо схожу функцію np.arange().
NumPy linspace() проти NumPy arange()
Користувачі NumPy, ймовірно, вже стикалися з np.arange() для генерації послідовності чисел у заданому інтервалі.
Функція np.arange(start, stop, step) створює масив чисел від start до stop (не включаючи його), з кроком step; за замовчуванням крок дорівнює 1.
Однак, розмір кроку не завжди очевидний. Розглянемо, чому це так.
Наприклад, якщо потрібно отримати 4 рівномірно розподілені числа від 0 до 1, крок повинен дорівнювати 0.25. При використанні np.arange() значення 1 не буде включено до масиву. Отже, потрібно задати такий інтервал, щоб він перевищував значення stop.
Наступне зображення показує приклади, де потрібно отримати певну кількість рівновіддалених точок в інтервалі [a, b].
Рівномірно розташовані точки у діапазоні
Перший приклад з 4 точками між [0, 1] був простий. Ми знаємо, що крок між точками повинен дорівнювати 0.25.
Розглянемо складніший приклад, де потрібно отримати 7 рівновіддалених точок між 1 і 33. Значення кроку тут не є очевидним. Хоча його можна розрахувати вручну.
Проте, np.linspace() робить цю задачу значно простішою! 😄

За допомогою np.linspace() потрібно лише вказати потрібну кількість точок в діапазоні. Розмір кроку обчислюється автоматично.
З таким розумінням, перейдемо до вивчення синтаксису NumPy linspace().
Синтаксис NumPy linspace()
Синтаксис функції NumPy linspace() виглядає так:
np.linspace(start, stop, num, endpoint, retstep, dtype, axis)
На перший погляд, цей синтаксис може здатися складним через велику кількість параметрів.
Більшість з них є необов’язковими, і ми швидко перейдемо до спрощеного варіанту синтаксису.
Розглянемо параметри:
startіstop– початкова та кінцева точки інтервалу. Ці значення можуть бути як скалярами, так і масивами. В нашому керівництві ми обмежимось скалярними значеннями.num– кількість рівномірно розподілених точок. Це необов’язковий параметр зі значенням за замовчуванням 50.endpoint– необов’язковий параметр типуboolean, може мати значенняTrueабоFalse.- За замовчуванням його значення
True, тобто кінцева точка включена в інтервал. При значенніFalse, кінцева точка виключається. retstep– необов’язковий параметрboolean. Якщо його значенняTrue, повертається розмір кроку.dtype– тип даних чисел в масиві. Зазвичай тип виводиться як float і не потрібно вказувати його явно.axis– необов’язковий параметр, що визначає вісь, вздовж якої мають зберігатися числа. Це актуально лише у випадку, якщо початкове та кінцеве значення є масивами.
▶️ Що повертає функція np.linspace()?
Вона повертає N-вимірний масив рівномірно розподілених чисел. Якщо параметр retstep має значення True, також повертається розмір кроку.
Спираючись на попередні пояснення, ось спрощений синтаксис функції np.linspace():
np.linspace(start, stop, num)
Цей код поверне масив із num рівномірно розподілених чисел в діапазоні [start, stop].
Тепер, коли ми розглянули синтаксис, перейдемо до прикладів кодування.
Як створити рівномірно розподілені масиви за допомогою NumPy linspace()
#1. Створимо масив з 20 рівномірно розподіленими числами в інтервалі [1, 5].
Ви можете вказати значення start, stop та num як ключові аргументи. Це показано в коді нижче:
import numpy as np
arr1 = np.linspace(start = 1,stop = 5,num = 20)
print(arr1)
# Output:
# [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
# 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
# 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
# 4.78947368 5. ]
Зверніть увагу, що числа в масиві починаються з 1 і закінчуються 5, включаючи обидві кінцеві точки. Також зауважте, що числа, включаючи 1 та 5, представлені як float в масиві.
#2. В попередньому прикладі ми передали значення для start, stop та num як аргументи ключових слів. Якщо ви передаєте аргументи у правильному порядку, ви можете використовувати їх як позиційні аргументи, як показано нижче.
import numpy as np
arr2 = np.linspace(1,5,20)
print(arr2)
# Output:
# [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
# 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
# 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
# 4.78947368 5. ]
#3. Створимо ще один масив, де встановимо для параметра retstep значення True.
Це означає, що функція поверне масив і крок. Ми можемо розпакувати їх у дві змінні: arr3 – масив та step_size – розмір кроку.
Код нижче демонструє це.
import numpy as np
arr3, step_size = np.linspace(1,5,20,retstep = True)
print(arr3)
# Output:
# [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
# 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
# 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
# 4.78947368 5. ]
# Output:
print(step_size)
# 0.21052631578947367
#4. Наостанок, встановимо для endpoint значення False і подивимось, що буде.
import numpy as np
arr4 = np.linspace(1,5,20,endpoint = False)
print(arr4)
# Output:
# [1. 1.2 1.4 1.6 1.8 2. 2.2 2.4 2.6 2.8 3. 3.2 3.4 3.6 3.8
# 4. 4.2 4.4 4.6 4.8]
В результаті ви бачите, що 1 включено до масиву, а 5 – ні. Останнє значення масиву дорівнює 4.8, і у нас все ще є 20 чисел.
Поки що ми генерували тільки масиви з рівномірно розподіленими числами. У наступному розділі ми візуалізуємо ці числа.
Візуалізація рівномірно розподілених чисел у діапазоні
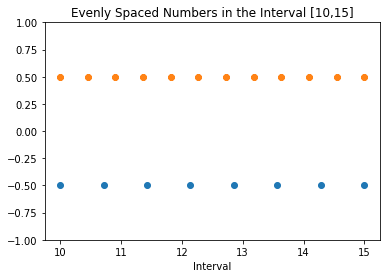
Розглянемо інтервал [10,15]. За допомогою np.linspace() створимо два масиви з 8 та 12 точками.
Далі, використаємо функцію побудови з бібліотеки matplotlib для їх візуалізації.
Для наглядності, зсунемо два масиви з N1 = 8 та N2 = 12 точками у різних позиціях осі y.
Код нижче демонструє це.
import numpy as np
import matplotlib.pyplot as plt
N1 = 8
N2 = 12
a = 10
b = 15
y1 = np.zeros(N1)
y2 = np.zeros(N2)
x1 = np.linspace(a, b, N1)
x2 = np.linspace(a, b, N2)
plt.plot(x1, y1-0.5, 'o')
plt.plot(x2, y2 + 0.5, 'o')
plt.ylim([-1, 1])
plt.title(f'Рівномірно розподілені числа в діапазоні [{a},{b}]')
plt.xlabel('Діапазон')
plt.show()
Створення рівномірно розподілених точок може бути корисним при роботі з математичними функціями. Розглянемо це далі.
Використання NumPy linspace() з математичними функціями
Згенерувавши масив з рівномірно розподіленими числами за допомогою np.linspace(), можна обчислити значення математичних функцій у діапазоні.
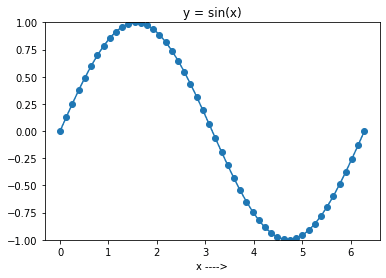
У коді нижче спочатку генеруються 50 рівномірно розподілених точок у діапазоні від 0 до 2π. Потім, створюється масив y за допомогою np.sin() для масиву x. Зверніть увагу, що можна не вказувати параметр num, оскільки за замовчуванням його значення 50. Але ми все одно вкажемо його явно.
На наступному кроці можна побудувати графік синусоїди в діапазоні [0, 2π]. Для цього використаємо matplotlib, як у попередньому прикладі. Функція plot() з matplotlib.pyplot використовується для створення лінійного графіка.
import numpy as np
import matplotlib.pyplot as plt
N = 50
a = 0.0
b = 2*np.pi
x = np.linspace(a, b, N)
y = np.sin(x)
plt.plot(x, y, marker = "o")
plt.ylim([-1, 1])
plt.title(f'y = sin(x)')
plt.xlabel('x ---->')
plt.show()
Тепер запустіть код, встановивши N рівним 10. Ви отримаєте графік, як показано на малюнку нижче.
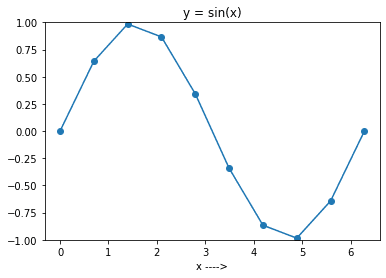
Як бачимо, графік вийшов не дуже гладким, оскільки ми вибрали лише 10 точок у діапазоні.
Загалом, чим більшу кількість точок ви виберете, тим гладкішим буде графік функції.
Висновок
Підсумуємо, що ми вивчили.
np.linspace(start, stop, num)повертає масив зnumрівномірно розподілених чисел в діапазоні [start,stop].- Встановіть необов’язковий параметр
endpointнаFalse, щоб виключити кінцеву точку, і отримайте інтервал [start,stop). - Встановіть параметр
retstepнаTrue, щоб отримати розмір кроку. - Генеруйте рівномірно розподілені масиви за допомогою
np.linspace(), і використовуйте їх з математичними функціями.
Сподіваємося, що тепер ви розумієте, як працює np.linspace(). Ви можете запустити ці приклади в блокноті Jupyter. Ознайомтеся з нашим посібником по Jupyter або розгляньте інші альтернативи Jupyter.
До зустрічі в наступному уроці з Python. А поки продовжуйте кодувати! 😀