Цей підручник навчить вас, як написати програму на Python, щоб перевірити, чи число є простим чи ні.
Якщо ви коли-небудь проходили тести з програмування, ви натрапили на математичне запитання в тесті на простоту чи перевірку того, чи число є простим. І протягом наступних кількох хвилин ви навчитеся придумувати оптимальне рішення цього питання.
У цьому посібнику ви:
- повторити основи простих чисел,
- написати код Python, щоб перевірити, чи число є простим, і
- оптимізуйте його далі, щоб отримати алгоритм виконання O(√n).
Для всього цього та іншого давайте почнемо.
Що таке просте число?
Почнемо з огляду основ простих чисел.
У теорії чисел — натуральне число n простий якщо воно має рівно два множники: 1 і саме число (n). Згадайте зі шкільної математики: число i називається множником числа n, якщо i ділить n порівну. ✅
У наступній таблиці наведено кілька чисел, усі їхні множники та чи є вони простими.
nЧильники є простими? 11No21, 2Yes31, 3Yes41, 2, 4No71, 7Yes151, 3, 5, 15No
З наведеної вище таблиці ми можемо записати наступне:
- 2 — найменше просте число.
- 1 є множником кожного числа.
- Кожне число n є множником саме по собі.
Отже, 1 і n є тривіальними множниками для будь-якого числа n. І просте число не повинно мати жодних множників, крім цих двох.
Це означає, що коли ви переходите від 2 до n – 1, ви не зможете знайти нетривіальний множник, який ділить n без залишку.
O(n) Алгоритм для перевірки, чи число є простим у Python
У цьому розділі давайте формалізуємо наведений вище підхід у функцію Python.
Ви можете прокрутити всі числа від 2 до n – 1 за допомогою об’єкта range() у Python.
У Python діапазон (початок, зупинка, крок) повертає об’єкт діапазону. Потім ви можете виконати ітерацію по об’єкту діапазону, щоб отримати послідовність від початку аж до зупинки -1 з кроком.
Оскільки нам потрібен набір цілих чисел від 2 до n-1, ми можемо вказати діапазон (2, n) і використовувати його в поєднанні з циклом for.
Ось що ми хотіли б зробити:
- Якщо ви знайдете число, яке ділить n порівну без залишку, ви можете відразу зробити висновок, що це число не є простим.
- Якщо ви прокрутили весь діапазон чисел від 2 аж до n – 1, не знайшовши числа, яке ділить n порівну, тоді число є простим.
Функція Python для перевірки простого числа
Використовуючи вищесказане, ми можемо продовжити та визначити функцію is_prime() наступним чином.
def is_prime(n):
for i in range(2,n):
if (n%i) == 0:
return False
return True
Давайте тепер розберемо наведене вище визначення функції.
- Наведена вище функція is_prime() приймає натуральне число n як аргумент.
- Якщо ви знайдете множник у вказаному діапазоні (2, n-1), функція повертає False, оскільки число не є простим.
- І він повертає True, якщо ви проходите весь цикл, не знаходячи фактора.
Далі викличемо функцію з аргументами та перевіримо, чи правильний результат.
is_prime(2) # True is_prime(8) # False is_prime(9) # False is_prime(11) # True
У вихідних даних вище ви бачите, що 2 і 11 є простими (функція повертає True). А 8 і 9 не є простими (функція повертає False).
Як оптимізувати функцію Python is_prime()
Тут ми можемо зробити невелику оптимізацію. Зверніть увагу на перелік факторів у таблиці нижче.
NumberFactors61, 2, 3, 6101, 2, 5, 10181, 2, 3, 6, 9, 18
Отже, ми бачимо, що єдиний множник n, який більший за n/2, це саме n.
Отже, це означає, що вам не потрібно виконувати цикл до n – 1. Натомість ви можете запустити цикл лише до n/2.
Якщо ви не знайдете нетривіальний множник до n/2, ви також не зможете знайти такий, що перевищує n/2.
Тепер модифікуємо функцію is_prime(), щоб перевірити фактори в діапазоні (2, n/2)
def is_prime(n):
for i in range(2,int(n/2)):
if (n%i) == 0:
return False
return True
Давайте перевіримо результат за допомогою кількох викликів функцій.
is_prime(9) # False is_prime(11) # True
Незважаючи на те, що може здатися, що ми оптимізували, цей алгоритм не ефективніший за попередній з точки зору складності виконання. Фактично, обидва вони мають O(n) складність часу виконання: пропорційну значенню n або лінійну в n.
Чи можемо ми зробити краще? Так, ми можемо!
▶️ Перейдіть до наступного розділу, щоб визначити, як покращити часову складність для перевірки простих чисел.
O(√n) Алгоритм перевірки простого числа в Python
Буває, що множники числа зустрічаються парами.
Якщо a є множником числа n, то існує також такий множник b, що axb = n, або просто ab = n.
Переконаємося в цьому на прикладі.
У таблиці нижче наведено множники числа 18, що зустрічаються в парах. Ви можете підтвердити те саме для кількох інших номерів, якщо хочете.
Також зауважте, що √18 дорівнює приблизно 4,24.
А в факторах, які зустрічаються в парах (a, b), ви можете побачити, що якщо a менше 4,24, то b більше 4,24—у цьому прикладі (2, 18) і (3, 6).
Множники числа 18 попарно
На малюнку нижче показано множники числа 18, нанесені на числову пряму.
Якщо число n є повним квадратом, ви матимете a = b = √n як один із множників.
▶️ Подивіться на множники 36 у таблиці нижче. Оскільки 36 є повним квадратом, a = b = 6 є одним із множників. Для всіх інших пар факторів (a, b) виконується a < 6 і b > 6.
Множники числа 36 попарно
Підводячи підсумок, маємо наступне:
- Кожне число n можна записати як n = axb
- Якщо n — повний квадрат, то a = b = √n.
- А якщо a < b, то a < √n і b > √n.
- Інакше, якщо a > b, то a > √n і b < √n.
Тож замість того, щоб перебирати всі цілі числа до n/2, ви можете вибрати виконання до √n. І це набагато ефективніше, ніж наш попередній підхід.
Як змінити алгоритм is_prime() на O(√n).
Давайте приступимо до оптимізації функції для перевірки простих чисел у Python.
import math
def is_prime(n):
for i in range(2,int(math.sqrt(n))+1):
if (n%i) == 0:
return False
return True
Тепер розберемо наведене вище визначення функції:
- Щоб обчислити квадратний корінь із числа, давайте імпортуємо вбудований математичний модуль Python і використаємо функцію math.sqrt().
- Оскільки n може бути не ідеальним квадратом, нам доведеться перетворити його на ціле число. Використовуйте int(var), щоб перетворити var в int.
- Щоб переконатися, що ми справді перевіряємо √n, ми додаємо плюс один, оскільки функція range() за замовчуванням виключає кінцеву точку діапазону.
Комірка коду нижче перевіряє, чи наша функція is_prime() працює правильно.
is_prime(8) # False is_prime(15) # False is_prime(23) # True
У наступному розділі створимо кілька простих графіків, щоб візуально зрозуміти O(n) і O(√n).
Візуальне порівняння O(n) і O(√n).
▶️ Запустіть наведений нижче фрагмент коду в середовищі блокнота Jupyter за вашим вибором.
import numpy as np
import seaborn as sns
import pandas as pd
n = 20
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
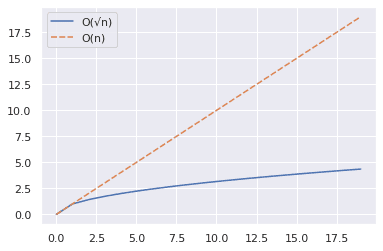
Наведений вище фрагмент показує, як можна побудувати криві для n і √n для діапазону значень.
- Ми використовуємо функцію NumPy arange(), щоб створити масив чисел.
- Потім ми збираємо значення n і √n до 20, але не включаючи, у pandas DataFrame.
- Далі малюємо за допомогою лінія Сіборна() функція.
З наведеного нижче графіка ми бачимо, що √n значно менше за n.
Давайте тепер збільшимо діапазон до 2000 і повторимо ті самі кроки, що й вище.
import numpy as np
import seaborn as sns
import pandas as pd
n = 2000
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
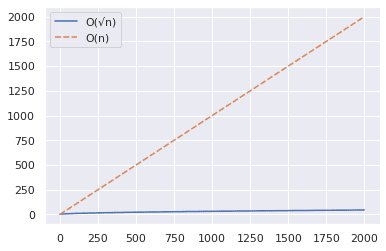
З наведеного вище графіка можна зробити висновок, що алгоритм O(√n) значно швидший, коли ви перевіряєте, чи велике число є простим.
Ось короткий приклад: 2377 є простим числом — переконайтеся в цьому!😀
У той час як підхід O(n) займає близько 2000 кроків, алгоритм O(√n) може допомогти отримати відповідь лише за 49 кроків.✅
Висновок
⏳ І настав час коротко підвести підсумки.
- Щоб перевірити, чи число є простим, наївний підхід полягає в тому, щоб прокрутити всі числа в діапазоні (2, n-1). Якщо ви не знайдете множник, який ділить n, то n є простим числом.
- Оскільки єдиним множником n, більшим за n/2, є саме n, ви можете запустити лише до n/2.
- Обидва вищезазначені підходи мають часову складність O(n).
- Оскільки множники числа зустрічаються парами, ви можете працювати лише до √n. Цей алгоритм набагато швидший, ніж O(n). І виграш помітний при перевірці, чи велике число є простим чи ні.
Сподіваюся, ви розумієте, як перевірити, чи число є простим у Python. Наступним кроком ви можете ознайомитися з нашим підручником із програм Python щодо операцій із рядками, де ви навчитеся перевіряти, чи є рядки паліндромами, анаграмами тощо.
До зустрічі в іншому підручнику. А поки бажаємо щасливого кодування!👩🏽💻
