Впровадження пошуку – це завжди виклик, але не неможлива задача.
У звичайному житті ми шукаємо, не дотримуючись жодного конкретного шаблону. Просто звертаємося до місць, де, на нашу думку, може знаходитися потрібне. Зазвичай ми не використовуємо жодної чіткої моделі.
Чи є такий підхід дієвим у світі програмування?
Ні! У програмах існують певні структури для пошуку даних. У цій статті ми розглянемо декілька алгоритмів, що використовують різні стратегії пошуку.
У сфері програмування існує чимало алгоритмів пошуку. Ми зупинимося на найважливіших і найбільш вживаних. Ознайомившись з ними, вам буде легше вивчати інші алгоритми.
У контексті цієї статті пошук означає знаходження елемента в масиві.
Розглянемо їх детальніше.
Лінійний пошук
Як випливає з назви, алгоритм лінійного пошуку використовує лінійний підхід для пошуку елементів у масиві. Він починає пошук з початку масиву та рухається до кінця, поки не знайде потрібний елемент. Програма завершує виконання, коли знаходить шуканий елемент.
Проілюструємо роботу лінійного пошуку на кількох прикладах для кращого розуміння.
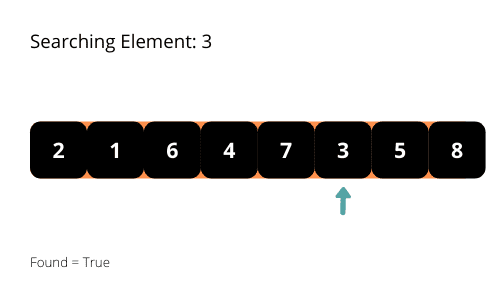
Якщо ви уважно проаналізуєте метод пошуку, ви помітите, що в найгіршому випадку час виконання програми становитиме O(n). При аналізі алгоритмів важливо розглядати найгіршу часову складність. Отже, часова складність лінійного пошуку – O(n).
Розглянемо реалізацію алгоритму лінійного пошуку.
Реалізація лінійного пошуку
Тепер, коли ви розумієте принцип роботи лінійного пошуку, настав час перейти до коду. Розглянемо спочатку кроки для реалізації лінійного пошуку. Спробуйте написати код самостійно. Не хвилюйтеся, якщо не вийде, я надам вам приклад коду.
Кроки для реалізації алгоритму лінійного пошуку:
- Ініціалізуйте масив елементами (наприклад, ваші улюблені числа).
- Створіть функцію під назвою `search_element`, яка приймає три аргументи: масив, довжину масиву та елемент, який потрібно знайти.
- `search_element(arr, n, element)`:
- Проітеруйте масив.
- Перевірте, чи збігається поточний елемент із шуканим.
- Якщо так, поверніть `True`.
- Якщо після завершення циклу функція все ще виконується, це означає, що елемент відсутній у масиві. Поверніть `False`.
- Проітеруйте масив.
- Виведіть повідомлення в залежності від значення, що повертає функція `search_element`.
Використовуючи наведені вище кроки, реалізуйте алгоритм лінійного пошуку.
Чи вдалося вам реалізувати алгоритм лінійного пошуку? Сподіваюся, що так. Якщо ви виконали завдання, перевірте свій код за допомогою прикладу нижче.
Якщо у вас не вийшло, не переживайте. Ознайомтеся з наведеним кодом, і ви побачите, як реалізувати цей алгоритм. Усе вийде!
## функція пошуку def search_element(arr, n, element): ## ітерація по масиву for i in range(n): ## перевірка, чи поточний елемент співпадає з шуканим if arr[i] == element: ## повернення True у випадку збігу return True ## якщо елемент не знайдено, виконання доходить сюди return False if __name__ == '__main__': ## ініціалізація масиву, його довжини та елемента для пошуку arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] n = 10 element_to_be_searched = 6 # element_to_be_searched = 11 if search_element(arr, n, element_to_be_searched): print(element_to_be_searched, "знайдено") else: print(element_to_be_searched, "не знайдено")
Спробуйте виконати програму спочатку з елементом, який є в масиві, а потім з елементом, якого в масиві немає.
Часова складність алгоритму лінійного пошуку становить O(n).
Чи можна її зменшити, використовуючи інші підходи?
Так, це можливо. Давайте розглянемо наступний алгоритм.
Двійковий пошук
Алгоритм двійкового пошуку постійно перевіряє середній елемент масиву. Цей алгоритм застосовується до відсортованих масивів.
Двійковий пошук переглядає масив і перевіряє середній елемент. Якщо він збігається з шуканим, програма завершує роботу. В іншому випадку, якщо середній елемент менший за шуканий, то з пошуку виключається ліва частина масиву. Якщо ж середній елемент більший, то виключається права частина масиву.
На кожній ітерації двійковий пошук зменшує область пошуку. Таким чином, кількість перевірок є меншою, ніж при лінійному пошуку.
Для кращого розуміння алгоритму двійкового пошуку, розгляньмо наступні ілюстрації.
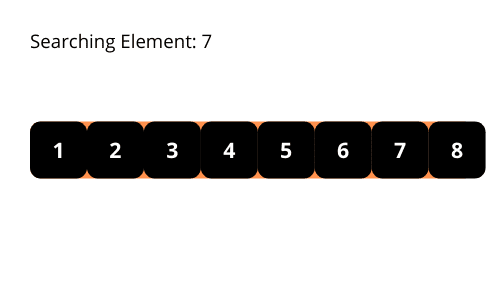
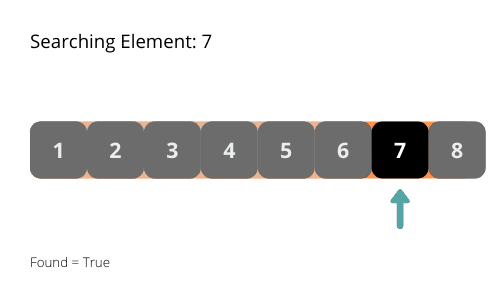
Часова складність алгоритму двійкового пошуку становить O(log n). На кожній ітерації область пошуку зменшується вдвічі. Це зменшення відбувається в геометричній прогресії.
Реалізація двійкового пошуку
Розглянемо спочатку кроки для реалізації двійкового пошуку, а потім перейдемо до коду. Кроки для реалізації алгоритму:
- Ініціалізуйте масив елементами (ваші улюблені числа).
- Створіть функцію `search_element`, яка приймає три аргументи: відсортований масив, довжину масиву та елемент для пошуку.
- `search_element(sorted_arr, n, element)`:
- Ініціалізуйте індексну змінну `i` для ітерації по масиву.
- Далі ініціалізуйте дві змінні для зберігання області пошуку в масиві. Назвемо їх `start` та `end`, оскільки вони позначають індекси.
- Виконуйте цикл, поки `i` менше за довжину масиву.
- Обчисліть середній індекс області пошуку, використовуючи значення `start` та `end`. Це буде `(start + end) // 2`.
- Перевірте, чи дорівнює елемент за середнім індексом шуканому.
- Якщо так, поверніть `True`.
- Інакше, якщо елемент за середнім індексом менший за шуканий елемент, перемістіть індекс `start` області пошуку до значення `middle + 1`.
- Інакше, якщо елемент за середнім індексом більший за шуканий, перемістіть індекс `end` області пошуку до значення `middle – 1`.
- Збільште індекс масиву `i`.
- Якщо після завершення циклу функція все ще виконується, елемент не знайдено у масиві. Поверніть `False`.
- Виведіть повідомлення залежно від значення, що повертає функція `search_element`.
Спробуйте написати код, аналогічно реалізації лінійного пошуку.
…
Чи отримали ви код?
Так, порівняйте його з кодом нижче. Якщо ні, не хвилюйтеся. Зрозумійте реалізацію, використовуючи наведений приклад коду.
## функція пошуку def search_element(sorted_arr, n, element): ## індекс масиву для ітерації i = 0 ## змінні для відстежування області пошуку ## ініціалізуємо їх початковим і кінцевим індексами start = 0 end = n - 1 ## ітерація по масиву while i < n: ## отримання індексу середнього елемента middle = (start + end) // 2 ## перевірка, чи збігається середній елемент з шуканим if sorted_arr[middle] == element: ## повертаємо True, оскільки елемент є в масиві return True elif sorted_arr[middle] < element: ## переміщуємо початковий індекс області пошуку вправо start = middle + 1 else: ## переміщуємо кінцевий індекс області пошуку вліво end = middle - 1 i += 1 return False if __name__ == '__main__': ## ініціалізація масиву, його довжини та елемента для пошуку arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] n = 10 element_to_be_searched = 9 # element_to_be_searched = 11 if search_element(arr, n, element_to_be_searched): print(element_to_be_searched, "знайдено") else: print(element_to_be_searched, "не знайдено")
Перевірте код у різних ситуаціях, коли елемент присутній і коли відсутній.
Висновок
Алгоритм двійкового пошуку є значно ефективнішим, ніж лінійний пошук. Для двійкового пошуку необхідно відсортувати масив, на відміну від лінійного пошуку. Сортування займає певний час, але використання ефективних алгоритмів сортування створює хорошу комбінацію з алгоритмом двійкового пошуку.
Тепер ви добре знайомі з найпоширенішими алгоритмами пошуку в Python.
Далі ознайомтеся з популярними інструментами для самостійного пошуку.
Вдалих вам розробок 🙂 🧑💻