Важливість сортування даних у програмуванні
Упорядкування списків даних є критично важливим аспектом обробки інформації в програмних застосунках. Це суттєво для наочного представлення даних та ефективного пошуку. Не дивно, що кожен кваліфікований програміст повинен володіти навичками сортування масивів. Ця стаття розглядає декілька поширених алгоритмів, які використовуються для сортування масивів у JavaScript.
Що таке сортування та для чого воно потрібне?
 Джерело: Unsplash
Джерело: Unsplash
Сортування – це процес впорядкування набору значень за заданою схемою. Ця схема може передбачати порядок від найменшого до найбільшого значення або навпаки. Сортування масивів у JavaScript корисне тим, що допомагає подати дані в більш структурованому вигляді.
Наприклад, користувач може захотіти бачити файли, відсортовані за часом їхньої модифікації, або товари, відсортовані за вартістю. Крім того, сортування є необхідним для ефективного бінарного пошуку даних, який працює лише зі впорядкованими даними.
Хоча існують готові функції та бібліотеки для спрощення процесу сортування, розуміння основних принципів роботи цих алгоритмів є важливим для проходження технічних співбесід або при необхідності написання низькорівневого коду.
Алгоритми сортування масивів у JavaScript
Сортування бульбашкою

Сортування бульбашкою є, ймовірно, найпростішим для розуміння та реалізації алгоритмом. Він працює шляхом багаторазового проходження масиву. При кожному проході ми ітеруємо по масиву від початку до кінця, порівнюючи кожні два сусідні елементи. Якщо елементи розміщені у неправильному порядку, ми змінюємо їх місцями.
Ми виконуємо n проходів, де n – кількість елементів у масиві. З кожним проходом масив стає все більш відсортованим, починаючи з кінця. Псевдокод для алгоритму сортування чисел у порядку зростання виглядає так:
1. Нехай n – кількість елементів у масиві
2. Виконати цикл n разів, використовуючи i для відстеження кількості ітерацій (виконуючи наступне у кожному циклі)
a. Пройти по масиву від другого елемента до (n - i)-го елемента
b. Якщо попередній елемент більший за поточний елемент, поміняти їх місцями.
Код на JavaScript виглядає наступним чином:
function sort(arr) {
const n = arr.length;
for (let i = 0; i < n; i++) {
for (let j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
const temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}
Для кращого розуміння процесу, рекомендується додати виведення console.log всередині двох циклів, щоб спостерігати за зміною масиву під час кожної ітерації.
У наведеному нижче коді функцію сортування було модифіковано для додавання console.log у два цикли. Також створено невеликий невідсортований масив, який сортується за допомогою цієї функції.
function sort(arr) {
const n = arr.length;
for (let i = 0; i < n; i++) {
console.log(`Pass: ${i}`);
for (let j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
const temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
console.log(arr);
}
}
return arr;
}
const array = [9, 2, 7, 4, 1];
sort(array);
console.log(array);
Результатом виконання наведеного коду буде:

Сортування бульбашкою має часову складність O(n^2), оскільки він виконує n проходів, кожен з яких ітерує по масиву. Тому він є неефективним для великих масивів. Однак, він має просторову складність O(1), оскільки змінює елементи масиву на місці.
Сортування вставками

Сортування вставками – це поширений алгоритм для сортування масивів JavaScript. Припустимо, ми використовуємо сортування вставками для сортування значень у порядку зростання. Алгоритм працює, вибираючи число, яке ми називатимемо num. Потім він переміщує num ліворуч, доки кожне інше число ліворуч від num не стане меншим за num. Всі числа будуть відсортовані, якщо це зробити від другого елемента до кінця. Ось опис у псевдокоді.
1. Нехай n – кількість елементів у масиві
2. Цикл i від 1 до n-1 (починаючи з другого елемента)
a. Встановити currentElement на array[i]
b. Встановити j на i-1
c. Поки j >= 0 і array[j] > current_element
i. Перемістити array[j] до array[j+1]
ii. Зменшити j на 1
d. Встановити array[j+1] на current_element
А тепер псевдокод, реалізований у JavaScript, виглядає так.
function insertionSort(array) {
const n = array.length;
for (let i = 1; i < n; i++) {
const currentElement = array[i];
let j = i - 1;
while (j >= 0 && array[j] > currentElement) {
array[j + 1] = array[j];
j -= 1;
}
array[j + 1] = currentElement;
}
return array;
}
Як і у випадку з сортуванням бульбашкою, додавання console.log допомагає візуалізувати процес. Наведений нижче код демонструє роботу сортування вставками.
function sort(array) {
const n = array.length;
for (let i = 1; i < n; i++) {
const currentElement = array[i];
let j = i - 1;
console.log("Placing element:", currentElement);
while (j >= 0 && array[j] > currentElement) {
array[j + 1] = array[j];
j -= 1;
}
array[j + 1] = currentElement;
console.log("Placed it at position:", j + 1);
console.log(array);
}
return array;
}
const array = [4, 1, 2, 5, 3];
sort(array);
Запуск наведеного коду дасть такий результат:
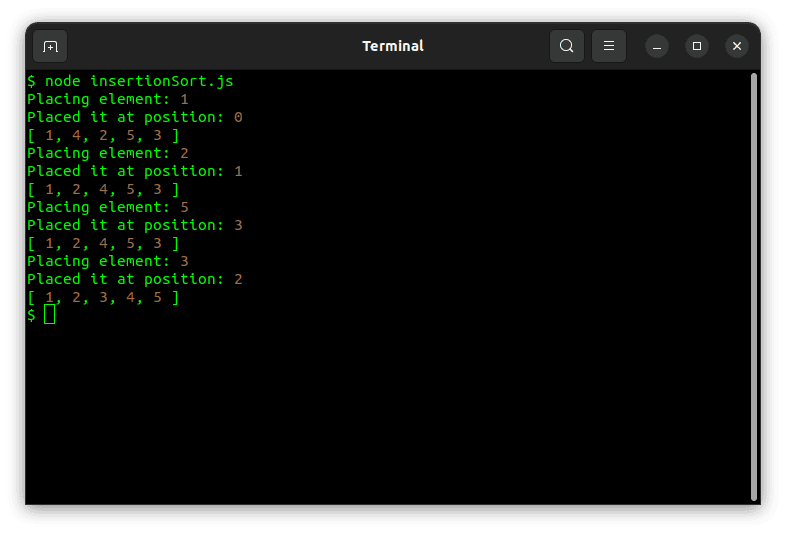
Сортування злиттям

У той час як сортування вставками та бульбашкою мають квадратичну часову складність, сортування злиттям має квазілінійну. Його часова складність O(n * log(n)).
Сортування злиттям використовує підхід “розділяй та володарюй”. Масив багаторазово поділяється на менші масиви по 1 елементу кожен. Після поділу, вони знову зливаються.
Поділ є рекурсивним, отже масив може бути згодом повторно зібраний.
Під час об’єднання масиву підмасиви об’єднуються у відсортованому порядку. Об’єднання виконується подібно до злиття двох відсортованих масивів. Псевдокод для цього процесу:
1. Якщо довжина масиву 1 або менше, повернути масив (базовий випадок)
2. Знайти середній індекс:
a. Встановити mid на округлення (довжина масиву / 2)
3. Розділити масив на два підмасиви:
a. Створити leftArray та скопіювати в нього першу половину масиву (від індексу 0 до mid)
b. Створити rightArray та скопіювати в нього другу половину масиву (від індексу mid+1 до кінця)
4. Рекурсивно викликати MergeSort для leftArray
5. Рекурсивно викликати MergeSort для rightArray
6. Об’єднати два відсортованих підмасиви:
a. Створити порожній resultArray
b. Поки leftArray та rightArray не є порожніми:
i. Якщо перший елемент у leftArray менший або рівний першому елементу в rightArray, додати його до resultArray
ii. В іншому випадку, додати перший елемент з rightArray до resultArray
c. Додати усі елементи що залишилися в leftArray до resultArray (якщо є)
d. Додати усі елементи що залишилися в rightArray до resultArray (якщо є)
7. Повернути resultArray
Реалізація цього алгоритму на JavaScript матиме такий вигляд:
function sort(array) {
// Базовий випадок, коли ми припиняємо поділ масиву
if (array.length == 1) {
return array;
}
// Знаходимо середню точку масиву
const m = Math.round(array.length / 2);
// Розділяємо масив на дві половини
const leftUnsorted = array.slice(0, m);
const rightUnsorted = array.slice(m);
// Рекурсивно викликаємо merge sort
const leftSorted = sort(leftUnsorted);
const rightSorted = sort(rightUnsorted);
// Повертаємо злитий відсортований масив
return merge(leftSorted, rightSorted);
}
function merge(left, right) {
// Об'єднуємо два відсортовані списки
let result = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex += 1;
} else {
result.push(right[rightIndex]);
rightIndex += 1;
}
}
return result.concat(left.slice(leftIndex), right.slice(rightIndex));
}
Запуск коду з прикладом масиву має спрацювати.
Швидке сортування

Подібно до сортування злиттям, швидке сортування використовує підхід “розділяй і володарюй”. Алгоритм вибирає опорний елемент. Потім він переміщує всі елементи, більші за опорний, праворуч, а менші – ліворуч. Після цього, опорний елемент опиняється у правильній позиції.
Для переміщення елементів відносно опорного, алгоритм спочатку переміщує опорний елемент в кінець масиву.
Після переміщення, ми використовуємо покажчик для ітерації з лівого боку масиву, шукаючи перше число, більше за опорне. Одночасно, інший покажчик ітерує з правого боку масиву, шукаючи перше число, менше за опорне. Коли обидва числа знайдені, ми міняємо їх місцями. Ця процедура повторюється, поки лівий покажчик не стане більшим за правий.
Коли ми зупиняємось, ми міняємо місцями більше з двох останніх чисел, поміняних місцями з опорним. У цей момент опорний елемент буде у правильній позиції; числа, менші за опорний елемент будуть зліва, а більші – справа.
Ця процедура повторюється рекурсивно для підмасивів зліва і справа від опорного елемента, до тих пір, поки в підмасиві не залишиться тільки один елемент.
Ось псевдокод для швидкого сортування:
1. Якщо lessThanPointer менше ніж greaterThanPointer: a. Вибрати опорний елемент з масиву b. Перемістити елементи так, щоб елементи менші були зліва, а більші – справа: c. Рекурсивно викликати Quicksort на лівому підмасиві d. Рекурсивно викликати Quicksort на правому підмасиві
І його реалізація на JavaScript:
function sort(array, low, high) {
if (low < high) {
// Вибір опорного індексу та розділення масиву
const pivotIndex = move(array, low, high);
// Рекурсивне сортування підмасивів ліворуч та праворуч від опорного елемента
sort(array, low, pivotIndex - 1);
sort(array, pivotIndex + 1, high);
}
}
function move(array, low, high) {
// Вибір опорного елемента (в цьому випадку останнього елемента)
const pivotElement = array[high];
// Ініціалізація індексу для меншого елемента
let i = low - 1;
for (let j = low; j < high; j++) {
// Якщо поточний елемент менший або рівний за опорний, поміняти його з елементом за індексом i+1
if (array[j] <= pivotElement) {
i += 1;
const temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
// Поміняти опорний елемент у правильну позицію
const temp = array[i];
array[i] = array[j];
array[j] = temp;
// Повернути індекс опорного елемента
return i + 1;
}
Сортування прикладу масиву за допомогою швидкого сортування в Node.js має дати наступне:
У кращому випадку швидке сортування виконується з квазілінійною часовою складністю. Використання пам’яті в швидкому сортуванні також масштабується логарифмічно. Тому він є відносно ефективним у порівнянні з іншими алгоритмами сортування масивів JavaScript.
Поради для ваших співбесід з кодування
❇️ Практика є ключовою. Це допоможе вам вивчити різні алгоритми, але, що більш важливо, це допоможе вам розвинути навички розв’язання проблем і обчислювального мислення. Ви також можете займатися на таких платформах, як Leetcode і AlgoExpert.
❇️ Спробуйте спочатку вирішити проблему самостійно. Замість того, щоб відразу переходити до рішення, спробуйте вирішити її, оскільки це допоможе вам розвинути навички вирішення проблем.
❇️ Якщо проблема триває занадто довго, переходьте до рішення; ви все ще можете навчитися розв’язувати задачу з рішення. Більшість платформ для навчання пропонують рішення. ChatGPT або Google Bard також корисні для пояснення концепцій.
❇️ Крім того, не пишіть код відразу; проаналізуйте свої рішення та обдумайте їх, перш ніж писати код. Псевдокод також є корисним способом швидкого запису ідей.
Висновок
У цій статті ми розглянули найпопулярніші алгоритми сортування. Однак спочатку вивчення їх усіх може здатися складним завданням. Тому рекомендується використовувати різні джерела для вивчення, а не покладатися тільки на одне. Успішного кодування!
Далі, перевірте розуміння функції sorted в Python.