Існує певна частка сумнівів щодо точності більшості статистичних даних, навіть якщо процедури проводяться ретельно, а для тестування використовується надійне обладнання. Програма Excel пропонує інструменти для визначення невизначеності, базуючись на стандартному відхиленні вибірки.
В Excel є набір статистичних формул, які можна використовувати для розрахунку невизначеності. У цій статті ми розглянемо обчислення середнього арифметичного, стандартного відхилення та стандартної помилки. Також ми покажемо, як відобразити цю невизначеність на діаграмах у Excel.
Для демонстрації ми будемо використовувати наступний набір даних:
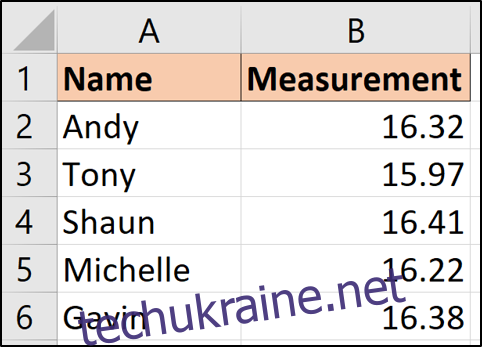
Цей набір даних ілюструє результати вимірювань, зроблених п’ятьма різними особами. З огляду на п’ять різних показань, існує невизначеність щодо істинного значення.
Обчислення середнього арифметичного
Коли існує невизначеність у діапазоні різних значень, використання середнього значення (середнього арифметичного) може слугувати надійним наближенням.
В Excel це легко зробити за допомогою функції AVERAGE.
Для наведеного вище прикладу можна застосувати наступну формулу:
=AVERAGE(B2:B6)
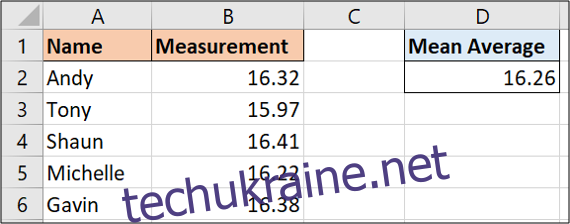
Розрахунок стандартного відхилення
Функції стандартного відхилення показують, наскільки широко розкидані дані навколо їхньої центральної точки (середнього значення, яке ми обчислили раніше).
Excel має кілька функцій стандартного відхилення для різних цілей. Дві основні – STDEV.P і STDEV.S.
Обидві функції обчислюють стандартне відхилення, але STDEV.P використовується, коли ви маєте всю сукупність даних, а STDEV.S – коли у вас є лише вибірка цієї сукупності.
У нашому прикладі ми використовуємо всі п’ять значень з набору даних, тому застосуємо STDEV.P.
Ця функція використовується так само, як і AVERAGE. Ось формула для нашого прикладу:
=STDEV.P(B2:B6)
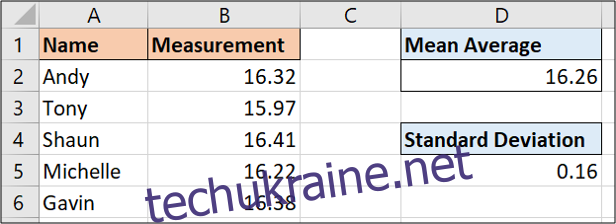
Результатом обчислення є 0,16. Це число показує, наскільки кожне окреме вимірювання зазвичай відрізняється від середнього значення.
Обчислення стандартної помилки
Після обчислення стандартного відхилення ми можемо визначити стандартну помилку.
Стандартна помилка – це стандартне відхилення, поділене на квадратний корінь кількості вимірювань.
Формула нижче розрахує стандартну помилку для наших даних:
=D5/SQRT(COUNT(B2:B6))
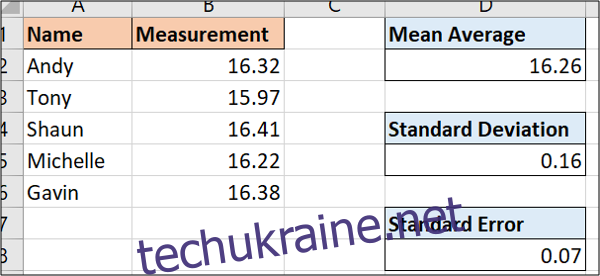
Відображення невизначеності на діаграмах за допомогою смуг похибок
В Excel дуже просто відобразити стандартні відхилення або межі невизначеності на діаграмах, використовуючи смуги похибок.
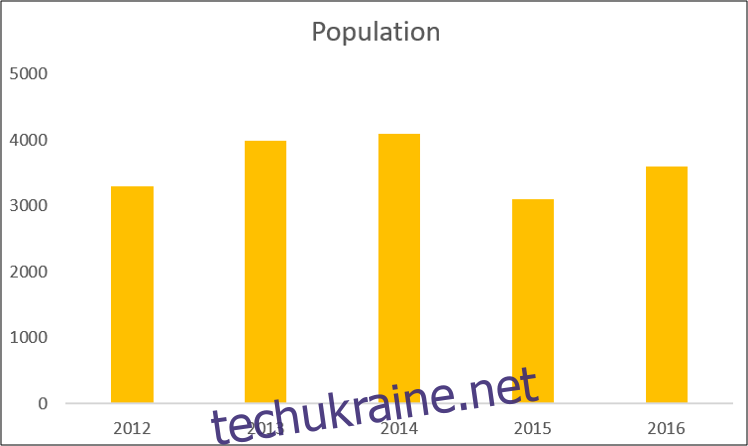
Нижче наведено гістограму з набору даних, що ілюструє сукупність, виміряну протягом п’яти років.
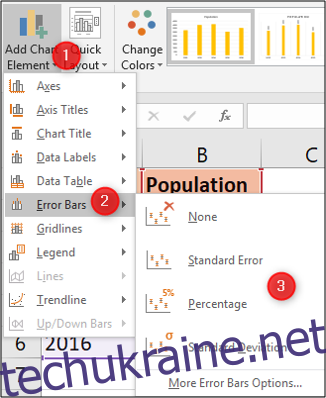
Вибравши діаграму, перейдіть до розділу “Конструктор” > “Додати елемент діаграми”.
Потім виберіть один із доступних типів смуг похибок.
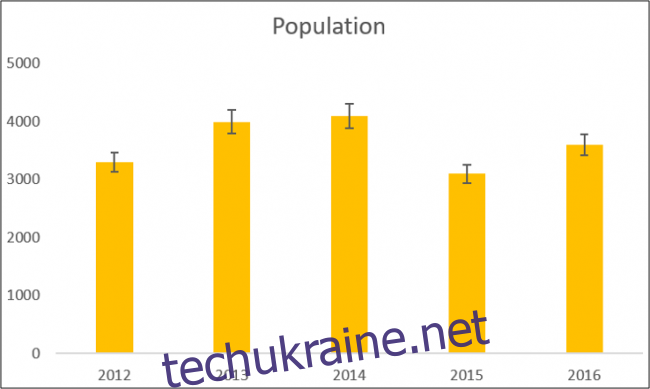
Можна відобразити стандартну помилку або значення стандартного відхилення, як ми обчислювали раніше, або ж відобразити похибку у відсотках (за замовчуванням 5%).
У цьому прикладі ми вирішили показати відсоток.
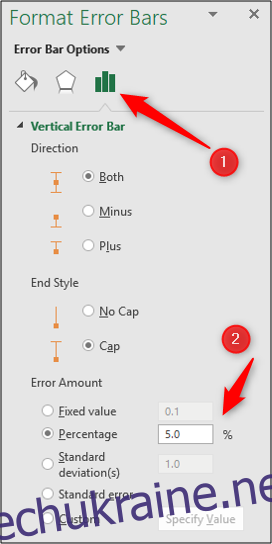
Існує кілька додаткових опцій для налаштування смуг похибок.
Двічі клацніть на смугу похибок на діаграмі, щоб відкрити панель “Формат смуг похибок”. Переконайтеся, що вибрано категорію “Параметри смуг похибок”.
Тут можна налаштувати відсоток, значення стандартного відхилення або навіть вибрати користувацьке значення з комірки, де може бути застосована статистична формула.
Excel є чудовим інструментом для статистичного аналізу та звітування. Він пропонує широкий набір інструментів для обчислення невизначеності, що дозволяє отримати необхідні результати.