Аналіз Big O – це методологія, що застосовується для оцінки та порівняння ефективності різних алгоритмів.
Завдяки цьому методу можна відібрати найбільш дієві та масштабовані алгоритмічні рішення. Цей матеріал є своєрідною шпаргалкою з Big O, де роз’яснюються ключові аспекти нотації Big O.
Що таке аналіз Big O?
Аналіз Big O – це метод для дослідження того, як змінюється продуктивність алгоритмів із збільшенням обсягу вхідних даних. Зокрема, нас цікавить, наскільки ефективним залишається алгоритм, коли розмір вхідних даних зростає.
Ефективність, у цьому контексті, визначається тим, наскільки раціонально використовуються ресурси системи для отримання результату. Головним чином нас цікавлять два види ресурсів: час і пам’ять.
Отже, під час аналізу Big O ми ставимо такі питання:
Відповідь на перше питання вказує на просторову складність алгоритму, а на друге – на його часову складність. Для вираження відповідей на ці запитання використовується спеціальна нотація, відома як нотація Big O. Про це докладніше йдеться далі в цій шпаргалці.
Необхідні знання
Для максимального використання цієї шпаргалки Big O, необхідно мати базове розуміння алгебри. Також, оскільки приклади будуть наведені на Python, бажано мати деяке ознайомлення з цим програмним середовищем. Однак глибоке розуміння не є обов’язковим, оскільки код не потрібно буде писати.
Як проводити аналіз Big O
У цьому розділі ми розглянемо методику виконання аналізу Big O.
При проведенні аналізу складності Big O важливо враховувати, що ефективність алгоритму залежить від структури вхідних даних.
Наприклад, алгоритми сортування показують найкращу продуктивність, коли дані вже впорядковані потрібним чином. Це – найкращий сценарій для роботи алгоритму. З іншого боку, ці ж алгоритми сортування працюють найповільніше, коли дані впорядковані у зворотному порядку. Це – найгірший сценарій.
Під час аналізу Big O ми розглядаємо лише найгірший сценарій.
Аналіз просторової складності

Почнемо нашу шпаргалку Big O з пояснення аналізу просторової складності. Ми аналізуємо, як зростає обсяг додаткової пам’яті, яку використовує алгоритм, зі збільшенням обсягу вхідних даних.
Наприклад, наведена нижче функція використовує рекурсію для ітерації від n до нуля. Її просторова складність прямо пропорційна n. Це відбувається тому, що зі збільшенням n, зростає і кількість викликів функції в стеку. Отже, вона має просторову складність O(n).
def loop_recursively(n):
if n == -1:
return
else:
print(n)
loop_recursively(n - 1)
Однак, більш ефективна реалізація виглядала б так:
def loop_normally(n):
count = n
while count >= 0:
print(count)
count =- 1
У наведеному вище алгоритмі ми створюємо лише одну додаткову змінну та використовуємо її для ітерації. Навіть якщо n стає все більшим і більшим, ми все одно використовуємо лише одну додаткову змінну. Тому цей алгоритм має постійну просторову складність, що позначається як “O(1)”.
Порівнюючи просторову складність двох наведених вище алгоритмів, ми можемо дійти висновку, що цикл while є більш ефективним, ніж рекурсія. Це є головною метою аналізу Big O: оцінити, як змінюються алгоритми зі збільшенням вхідних даних.
Аналіз часової складності

При аналізі часової складності, нас цікавить не загальний час виконання алгоритму, а зростання кількості обчислювальних кроків. Це пов’язано з тим, що фактичний час залежить від багатьох системних та випадкових факторів, які важко врахувати. Тому ми відстежуємо лише зростання кількості обчислювальних кроків, припускаючи, що кожен крок займає однакову кількість часу.
Для ілюстрації аналізу часової складності розглянемо такий приклад:
Припустимо, у нас є список користувачів, де кожен користувач має ідентифікатор і ім’я. Наше завдання – реалізувати функцію, яка повертає ім’я користувача за заданим ідентифікатором. Ось один із способів реалізації:
users = [
{'id': 0, 'name': 'Alice'},
{'id': 1, 'name': 'Bob'},
{'id': 2, 'name': 'Charlie'},
]
def get_username(id, users):
for user in users:
if user['id'] == id:
return user['name']
return 'User not found'
get_username(1, users)
Маючи список користувачів, алгоритм перебирає весь масив, щоб знайти користувача з відповідним ідентифікатором. Якщо у нас 3 користувачі, алгоритм виконує 3 ітерації. Якщо їх 10, він виконує 10.
Отже, кількість кроків прямо пропорційна кількості користувачів. Таким чином, алгоритм має лінійну часову складність. Однак, ми можемо покращити цей алгоритм.
Припустимо, що замість зберігання користувачів у списку, ми зберігаємо їх у словнику. Тоді наш алгоритм пошуку користувача виглядатиме так:
users = {
'0': 'Alice',
'1': 'Bob',
'2': 'Charlie'
}
def get_username(id, users):
if id in users:
return users[id]
else:
return 'User not found'
get_username(1, users)
Припустимо, що в цьому алгоритмі у словнику є 3 користувачі; ми виконаємо певну кількість кроків для отримання імені користувача. І припустимо, що у нас більше користувачів, скажімо, десять. Для отримання користувача ми виконаємо ту саму кількість кроків, що й раніше. Незалежно від кількості користувачів, кількість кроків для отримання імені залишається постійною.
Отже, цей новий алгоритм має постійну складність. Кількість виконаних обчислювальних кроків не залежить від кількості користувачів.
Що таке нотація Big O?
У попередньому розділі ми розглядали, як обчислюється просторова та часова складність Big O для різних алгоритмів. Для опису складності ми використовували такі терміни, як лінійна і постійна. Іншим способом опису складності є використання нотації Big O.
Нотація Big O – це спосіб представлення просторової або часової складності алгоритму. Нотація відносно проста: це літера O, за якою слідують дужки. У дужках ми пишемо функцію n, щоб позначити конкретну складність.
Лінійна складність позначається як n, тому ми запишемо її як O(n) (читається як “O від n”). Постійна складність позначається як 1, отже ми запишемо її як O(1).
Існують й інші види складності, про які ми поговоримо у наступному розділі. Загалом, для визначення складності алгоритму необхідно виконати такі кроки:
Отриманий результат буде виразом, який використовується у дужках.
Наприклад:
Розглянемо таку функцію на Python:
users = [
'Alice',
'Bob',
'Charlie'
]
def print_users(users):
number_of_users = len(users)
print("Total number of users:", number_of_users)
for i in number_of_users:
print(i, end=': ')
print(user)
Тепер обчислимо часову складність Big O для цього алгоритму.
Спочатку ми запишемо математичну функцію f(n), щоб представити кількість кроків обчислення, які виконує алгоритм. Пам’ятайте, що n – це розмір вхідних даних.
У нашому коді, функція виконує два кроки: один для обчислення кількості користувачів, а другий для друку цієї кількості. Потім для кожного користувача, вона виконує ще два кроки: один для друку індексу і другий для друку імені користувача.
Таким чином, функція, яка найкраще представляє кількість виконаних обчислювальних кроків, може бути записана як f(n) = 2 + 2n, де n – кількість користувачів.
Переходячи до другого кроку, вибираємо найбільш домінуючий член. 2n – це лінійний член, а 2 – постійний. Лінійний є більш домінуючим, ніж постійний, тому ми вибираємо 2n.
Отже, тепер наша функція f(n) = 2n.
Останнім кроком є видалення коефіцієнтів. У нашій функції, 2 є коефіцієнтом, тож ми його видаляємо. І функція стає f(n) = n. Це термін, який використовується у дужках.
Таким чином, часова складність нашого алгоритму дорівнює O(n), тобто лінійній складності.
Різні види складності Big O
В останньому розділі нашої шпаргалки Big O, показані різні види складності та відповідні графіки.
#1. Постійна

Постійна складність означає, що алгоритм використовує фіксований обсяг пам’яті (при аналізі просторової складності) або виконує постійну кількість кроків (при аналізі часової складності). Це є оптимальною складністю, оскільки алгоритму не потрібна додаткова пам’ять або час зі збільшенням обсягу вхідних даних. Тому він є дуже масштабованим.
Постійна складність позначається як O(1). Проте, не завжди можливо написати алгоритм, який працює з постійною складністю.
#2. Логарифмічна
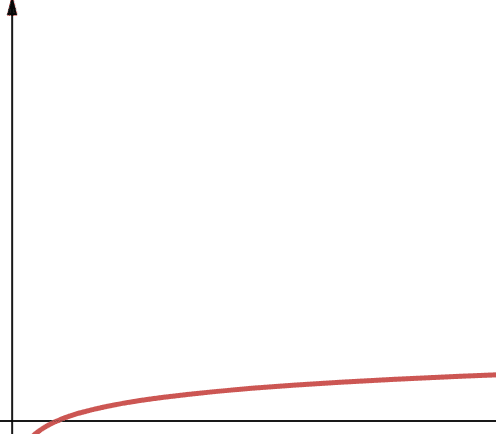
Логарифмічна складність позначається як O(log n). Важливо зазначити, що якщо основа логарифма не вказана в інформатиці, то за замовчуванням вважається, що вона дорівнює 2.
Отже, log n – це log2n. Логарифмічні функції відомі тим, що спочатку швидко зростають, а потім їх зростання сповільнюється. Це означає, що вони добре масштабуються і ефективно працюють із великими значеннями n.
#3. Лінійна
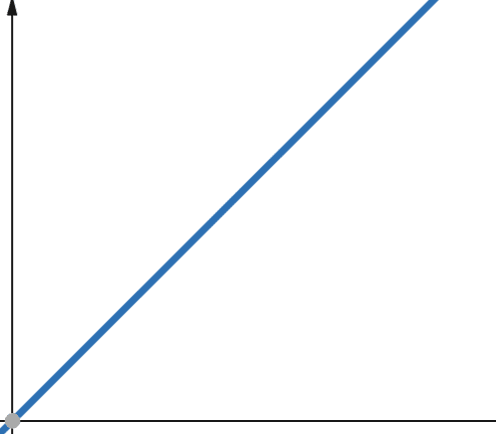
Для лінійних функцій, якщо незалежна змінна збільшується на коефіцієнт p, то залежна змінна також збільшується на той же коефіцієнт p.
Отже, функція з лінійною складністю зростає пропорційно розміру вхідних даних. Якщо розмір вхідних даних подвоюється, кількість обчислювальних кроків або використання пам’яті також подвоюється. Лінійна складність позначається як O(n).
#4. Лінеаритмічна
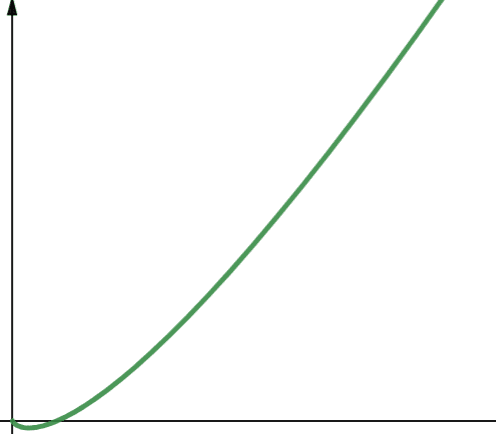
O(n * log n) представляє лінеаритмічну складність. Лінеаритмічна функція є лінійною функцією, помноженою на логарифмічну. Таким чином, лінеаритмічна функція дає дещо вищі значення, ніж лінійна функція, коли log n більше 1. Це відбувається тому, що n множиться на число більше 1.
Log n більше 1 для всіх значень n, більших за 2 (пам’ятайте, що log n – це log2n). Отже, для будь-якого значення n більшого за 2, лінеаритмічна складність менш масштабована, ніж лінійна. Оскільки в більшості випадків n більше 2, лінеаритмічні функції зазвичай менш масштабовані, ніж логарифмічні функції.
#5. Квадратична
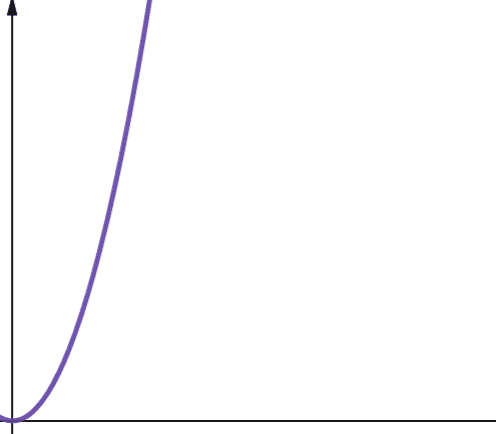
Квадратична складність позначається як O(n²). Це означає, що якщо розмір вхідних даних збільшиться у 10 разів, кількість виконаних кроків або використаного простору збільшиться у 10², тобто в 100 разів! Це не дуже масштабовано, і, як видно з графіка, складність зростає дуже швидко.
Квадратична складність виникає в алгоритмах, де є цикл, який виконується n разів, і для кожної ітерації цього циклу є ще один цикл, який також виконується n разів, наприклад, у Bubble Sort. Хоча в цілому це не ідеально, іноді немає іншого вибору, окрім як використовувати алгоритми з квадратичною складністю.
#6. Поліноміальна
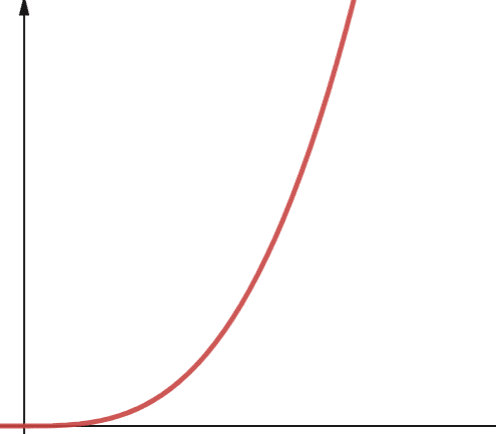
Алгоритм із поліноміальною складністю позначається як O(np), де p – деяке постійне ціле число. P – це степінь, до якого підноситься n.
Ця складність виникає, коли у вас є p вкладених циклів. Різниця між поліноміальною та квадратичною складністю полягає в тому, що квадратична складність має степінь 2, тоді як поліноміальна має будь-яке число більше 2.
#7. Експоненціальна
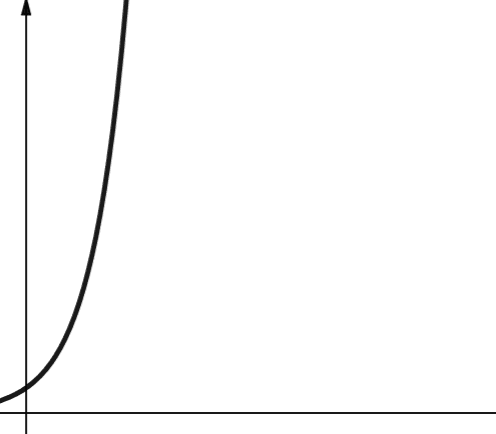
Експоненціальна складність зростає навіть швидше, ніж поліноміальна. У математиці, стандартним значенням для експоненціальної функції є константа e (число Ейлера). Проте в інформатиці, стандартне значення експоненціальної функції – 2.
Експоненціальна складність позначається як O(2n). Коли n дорівнює 0, 2n дорівнює 1. Але коли n збільшується до 5, 2n зростає до 32. Збільшення n на одиницю подвоює попереднє значення. Тому експоненціальні функції не дуже масштабовані.
#8. Факторіальна
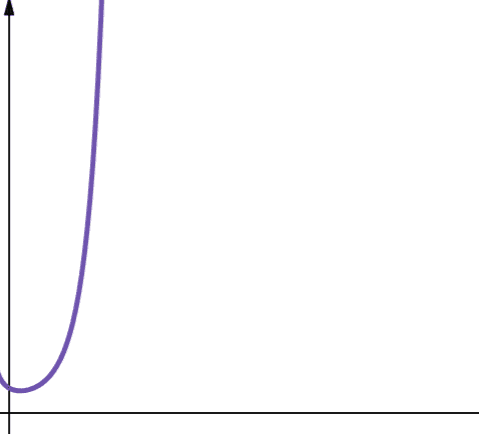
Факторіальна складність позначається як O(n!). Ця функція також зростає дуже швидко, тому вона не є масштабованою.
Висновок
У цій статті ми розглянули аналіз Big O та способи його обчислення. Ми також обговорили різні види складності та їх масштабованість.
Далі, ви можете потренуватися в аналізі Big O на прикладі алгоритму сортування на Python.