Машина опорних векторів (SVM) є одним з найбільш вживаних алгоритмів у царині машинного навчання. Її ефективність та здатність до навчання навіть на обмежених наборах даних роблять її особливо цінною. Але в чому ж її суть?
Що таке метод опорних векторів (SVM)?
SVM – це алгоритм машинного навчання, який використовує підхід навчання з учителем для побудови моделі, призначеної для двійкової класифікації. Звучить складно? У цій статті ми розкриємо суть SVM, зокрема її застосування в обробці природної мови. Але спочатку розгляньмо, як працює цей алгоритм.
Як функціонує SVM?
Уявімо просте завдання класифікації, де маємо дані з двома характеристиками, позначеними як x та y, а також один вихід – класифікацію, яка може бути або червоною, або синьою. Змоделюємо набір даних, який матиме наступний вигляд:
Враховуючи ці дані, наша мета полягає у визначенні межі прийняття рішення. Ця межа є лінією, яка розділяє точки даних на два класи. Ось той самий набір даних, але вже з проведеною межею рішення:
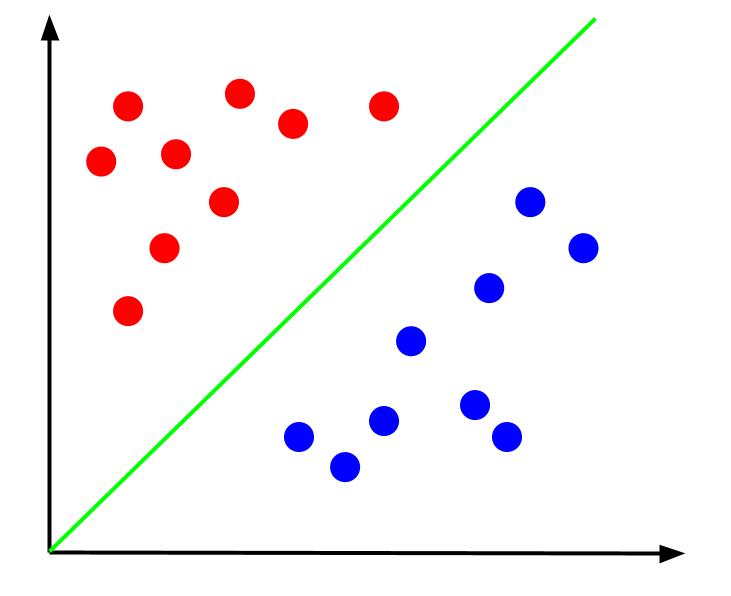
Використовуючи цю межу, ми можемо прогнозувати, до якого класу належить нова точка даних, залежно від її положення відносно цієї межі. Алгоритм SVM прагне створити оптимальну межу рішення, яка найкращим чином розділить ці класи.
Але що розуміється під “оптимальною” межею?
Оптимальною можна вважати ту межу рішення, яка максимізує відстань від неї до найближчих точок даних обох класів, так званих опорних векторів. Опорні вектори – це точки даних, що лежать найближче до межі рішення і становлять найбільший ризик неправильної класифікації через свою близькість до іншого класу.
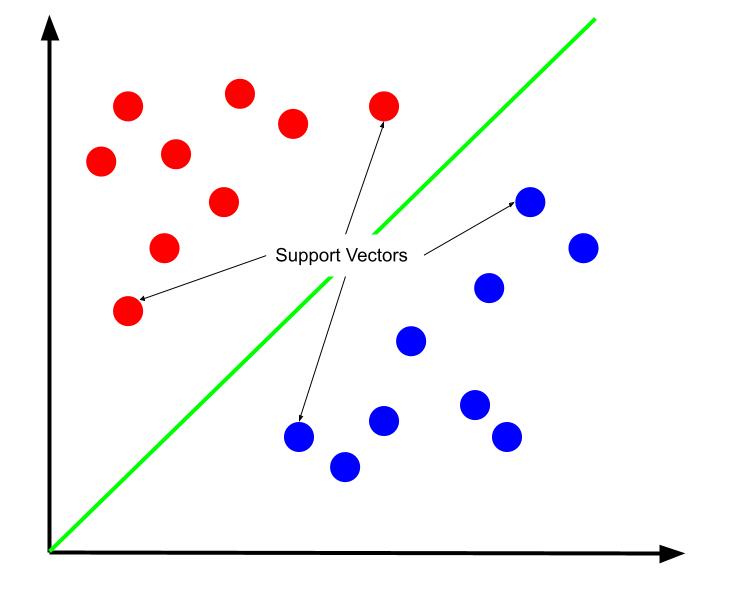
Отже, навчання SVM полягає у пошуку такої лінії, яка максимально збільшує простір між опорними векторами.
Важливо відзначити, що положення межі рішення визначається саме опорними векторами, тому всі інші точки даних є, по суті, зайвими. Таким чином, для навчання потрібні лише опорні вектори.
У цьому прикладі межа рішення є прямою лінією, оскільки набір даних має лише дві ознаки. Якщо набір даних має три ознаки, то межею рішення буде площина, а не лінія. А для чотирьох і більше ознак межа рішення називається гіперплощиною.
Нелінійно розділені дані
У наведеному прикладі ми мали справу з простими даними, які можна було розділити за допомогою лінійної межі рішення. Розглянемо інший сценарій, коли дані розташовані таким чином:
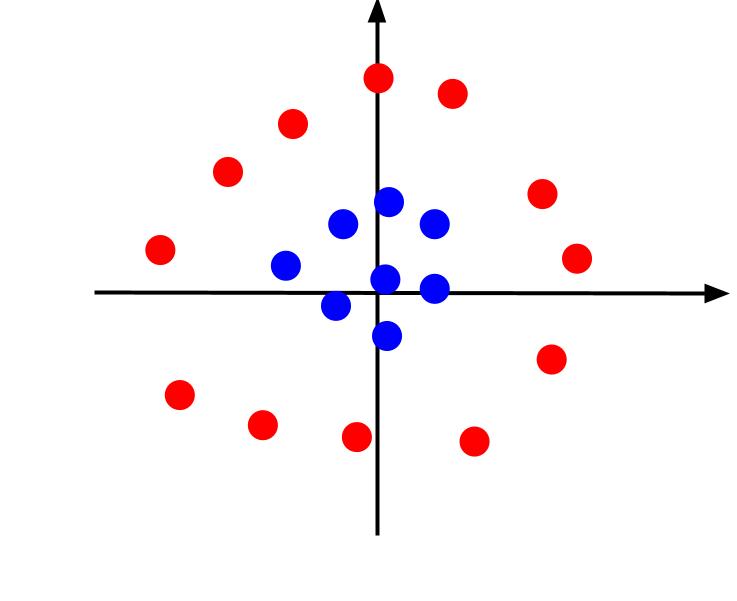
У цьому випадку розділити дані за допомогою прямої лінії неможливо. Але ми можемо створити додаткову функцію, z, визначену як: z = x^2 + y^2. Додавши z як третю вісь, ми перетворимо площину на тривимірний простір.
Якщо подивитися на тривимірний графік під таким кутом, щоб вісь x була горизонтальною, а z – вертикальною, отримаємо наступне зображення:
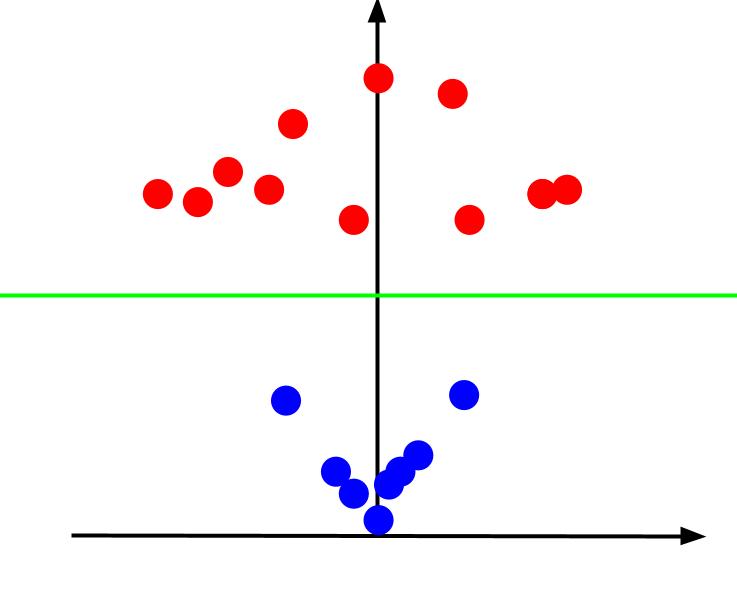
Значення z показує відстань точки від початку координат. Як результат, сині точки, що розташовані ближче до початку, матимуть менші значення z, тоді як червоні точки, що розташовані далі, матимуть більші значення z. Побудова графіка цих z-значень дає чітке лінійне розділення класів, як показано на малюнку.
Ця ідея є ключовою для SVM: відображення даних у вищий вимір, де точки можна розділити лінійною межею. Функції, що відповідають за це, називаються функціями ядра. Існує безліч ядерних функцій, таких як сигмоїдна, лінійна, нелінійна та RBF.
Для ефективнішого відображення цих функцій, SVM використовує так званий трюк ядра.
SVM у машинному навчанні
SVM є одним з численних алгоритмів, застосовуваних у машинному навчанні, нарівні з популярними методами, такими як “дерева рішень” та нейронні мережі. SVM вважають кращим вибором завдяки його хорошій продуктивності навіть з меншими обсягами даних. Найчастіше його використовують для:
- Класифікації тексту: розподіл текстових даних, таких як коментарі або відгуки, за заданими категоріями.
- Розпізнавання облич: аналіз зображень для виявлення облич, наприклад, для застосування фільтрів доповненої реальності.
- Класифікації зображень: SVM є ефективними для класифікації зображень порівняно з іншими методами.
Проблема класифікації тексту
Інтернет переповнений текстовими даними, більшість яких є неструктурованими та немаркованими. Для кращого використання і розуміння цих даних потрібна їх класифікація. Приклади застосування класифікації тексту:
- Класифікація твітів за темами, для зручного відстеження потрібної інформації.
- Розподіл електронних листів на категорії “соціальні мережі”, “акції” або “спам”.
- Класифікація коментарів на публічних форумах як “ненависницькі” або “непристойні”.
Як SVM працює з класифікацією природної мови
SVM використовується для класифікації тексту на такі, що належать до певної теми, та такі, що не належать. Це відбувається через попереднє перетворення текстових даних на набір з численними ознаками.
Один зі способів зробити це – створити ознаку для кожного слова в наборі даних. Тоді для кожної текстової точки даних ви записуєте кількість повторень кожного слова. Якщо в наборі даних зустрічаються, наприклад, унікальні слова, то ви матимете ознак в наборі.
Також ви маєте надати класифікації для цих точок даних. Хоча ці класифікації представлені текстом, більшість реалізацій SVM очікують числові мітки.
Тому, перед навчанням, вам необхідно перетворити текстові мітки на числа. Після підготовки набору даних та використання цих ознак як координат, ви можете застосувати модель SVM для класифікації тексту.
Створення SVM на Python
Для створення SVM у Python можна використовувати клас SVC з бібліотеки sklearn.svm. Ось приклад використання класу SVC для побудови моделі SVM на Python:
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
# Завантаження набору даних
X = ...
y = ...
# Розділення даних на навчальний та тестовий набори
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=19)
# Створення моделі SVM
model = SVC(kernel="linear")
# Навчання моделі на навчальних даних
model.fit(X_train, y_train)
# Оцінка моделі на тестових даних
accuracy = model.score(X_test, y_test)
print("Точність: ", accuracy)
У цьому прикладі ми спочатку імпортуємо клас SVC з бібліотеки sklearn.svm. Потім завантажуємо набір даних і розділяємо його на навчальну та тестову вибірки.
Далі створюємо модель SVM, ініціалізуючи об’єкт SVC та вказуючи тип ядра як “лінійний”. Потім навчаємо модель на навчальних даних, використовуючи метод fit, і оцінюємо модель на тестових даних, використовуючи метод score. Метод score повертає точність моделі, яку ми виводимо на консоль.
Ви також можете налаштувати інші параметри об’єкта SVC, наприклад параметр C, який керує силою регуляризації, та параметр gamma, який керує коефіцієнтом ядра для деяких ядер.
Переваги SVM
Ось деякі переваги використання машин опорних векторів:
- Ефективність: SVM є ефективними для навчання, особливо коли кількість зразків велика.
- Стійкість до шуму: SVM відносно стійкі до шуму в навчальних даних, оскільки вони намагаються знайти класифікатор з максимальним запасом, який менш чутливий до шуму, ніж інші методи.
- Ефективність пам’яті: SVM потребують лише підмножину навчальних даних у пам’яті, що робить їх ефективнішими за інші алгоритми.
- Ефективність у високорозмірних просторах: SVM можуть добре працювати, навіть якщо кількість ознак перевищує кількість зразків.
- Універсальність: SVM можна використовувати для задач класифікації та регресії, та вони можуть обробляти різні типи даних, включаючи лінійні та нелінійні.
Тепер розгляньмо кілька найкращих ресурсів для вивчення Support Vector Machine (SVM).
Навчальні ресурси
Вступ до опорних векторних машин
Книга “Вступ до опорних векторних машин” пропонує вичерпний і поступовий підхід до методів навчання на основі ядра.
Вона забезпечує міцну теоретичну основу для розуміння SVM.
Застосування опорних векторних машин
На відміну від першої книги, яка зосереджувалась на теорії, ця книга про застосування SVM приділяє увагу практичному застосуванню алгоритму.
В ній розглядається використання SVM в обробці зображень, виявленні шаблонів та комп’ютерному зорі.
Машини опорних векторів (інформатика та статистика)
Книга “Машини опорних векторів (інформатика та статистика)” надає огляд принципів ефективності SVM у різних застосуваннях.
Автори підкреслюють декілька факторів, які сприяють успіху SVM, включаючи їх здатність добре працювати з обмеженою кількістю налаштовуваних параметрів, стійкість до різних видів помилок і аномалій, а також ефективну обчислювальну продуктивність порівняно з іншими методами.
Навчання з ядрами
Книга “Навчання з ядрами” знайомить читачів з SVM та пов’язаними методами ядра.
Її мета – дати читачам базове розуміння математики та знання, необхідні для використання алгоритмів ядра в машинному навчанні. Книга пропонує детальний, але доступний вступ до SVM та методів ядра.
Підтримка векторних машин з Sci-kit Learn
Онлайн-курс “Підтримка векторних машин з Sci-kit Learn” від Coursera навчає, як реалізувати модель SVM за допомогою бібліотеки Sci-Kit Learn.

Крім того, ви ознайомитесь з теоретичною основою SVM, визначите їх сильні сторони та обмеження. Курс розрахований на початківців і займає близько 2,5 годин.
Підтримка векторних машин у Python: концепції та код
Платний онлайн-курс “Підтримка векторних машин у Python” від Udemy пропонує до 6 годин відеоінструкцій і видає сертифікат.

Він охоплює SVM і надійні методи їх реалізації на Python, а також бізнес-застосування Support Vector Machines.
Машинне навчання та штучний інтелект: підтримка векторних машин у Python
Цей курс з машинного навчання та штучного інтелекту навчає використанню SVM для різних застосувань, таких як розпізнавання зображень, виявлення спаму, медична діагностика та регресійний аналіз.

Ви будете застосовувати мову програмування Python для розробки ML-моделей для цих програм.
Заключні слова
У цій статті ми розглянули основні принципи роботи машин опорних векторів. Ми ознайомилися з їхнім застосуванням у машинному навчанні та обробці природної мови.
Ми також побачили приклад реалізації SVM за допомогою scikit-learn. Крім того, ми згадали про практичне застосування та переваги машин опорних векторів.
Хоча ця стаття була лише вступом, запропоновані ресурси допоможуть вам глибше вивчити SVM. Враховуючи їхню універсальність та ефективність, розуміння SVM є важливим для розвитку спеціаліста з даних або інженера з ML.
Наступним кроком може бути ознайомлення з найкращими моделями машинного навчання.