Як надрукувати трикутник Паскаля в Python

Зміст

Побудова трикутника Паскаля на Python: Повний посібник

У цьому посібнику ви освоїте створення трикутника Паскаля за допомогою мови Python для заданої кількості рядків.

Спочатку розглянемо основи побудови трикутника Паскаля. Далі перейдемо до розробки Python-функції та її оптимізації.

▶️ Розпочнімо!

Що таке трикутник Паскаля та як його будувати?

Виведення трикутника Паскаля для певної кількості рядків є популярною задачею на співбесідах з програмування.

У трикутнику Паскаля з n рядків, рядок під номером i містить i елементів.

Таким чином, у першому рядку розташований один елемент, який дорівнює 1. Кожен елемент у наступних рядках утворюється сумою двох чисел, які розташовані безпосередньо над ним.

На ілюстрації показано, як конструювати трикутник Паскаля з п’ятьма рядками.

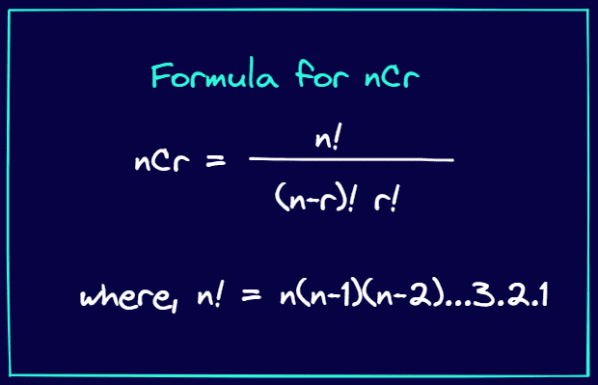
Зверніть увагу, що при необхідності можна додавати нулі, якщо над певним числом є лише одне число.

📝Спробуйте швидко створити трикутник Паскаля для n = 6 та n = 7, використовуючи описану вище процедуру.

Тепер перейдемо до написання коду. Ви можете використовувати Python IDE techukraine.net у своєму браузері для запуску фрагментів коду безпосередньо під час проходження цього посібника.

Python-функція для виведення трикутника Паскаля

У цьому розділі розробимо Python-функцію, яка виводить трикутник Паскаля для будь-якої заданої кількості рядків.

Нам потрібно розглянути два основних питання:

Яким чином виразити елементи у трикутнику Паскаля?
Як правильно вивести трикутник Паскаля з відповідним інтервалом і форматуванням?

Розглянемо ці питання зараз.

#1. Як обчислити значення елементів у трикутнику Паскаля?

Елементи трикутника Паскаля можна обчислити за допомогою формули nCr. З шкільного курсу математики відомо, що nCr представляє кількість способів вибору r елементів з множини n елементів.

Формула для nCr виглядає так:

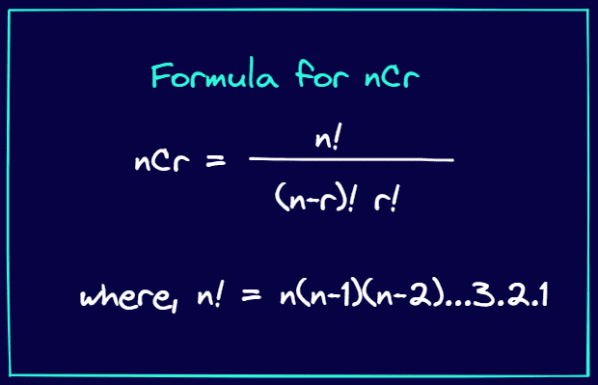
Тепер розглянемо, як виразити елементи в трикутнику Паскаля, використовуючи формулу nCr.

Отже, ми знайшли спосіб представити елементи матриці.

#2. Як налаштувати інтервали під час виведення?

У трикутнику Паскаля з numRows рядків, рядок №1 містить один елемент, рядок №2 – два елементи і так далі. Для виведення шаблону у формі трикутника, у рядку №i потрібно numRows – i пробілів. Використайте функцію діапазону Python у поєднанні з циклом for для цього.

Функція діапазону за замовчуванням виключає кінцеву точку, тому обов’язково додайте +1, щоб отримати потрібну кількість пробілів на початку.

Тепер, коли ми знаємо, як представляти елементи і як налаштувати пробіли для виведення трикутника Паскаля, визначимо функцію pascal_tri.

Аналіз визначення функції

Отже, що ми хочемо отримати від функції pascal_tri?

Функція pascal_tri повинна приймати кількість рядків (numRows) як аргумент.
Вона повинна виводити трикутник Паскаля з numRows.

Для обчислення факторіалу використаємо функцію factorial з вбудованого математичного модуля Python.

▶️ Запустіть наступний код для імпорту факторіалу та використання його у вашому поточному модулі.

from math import factorial

Фрагмент коду нижче містить визначення функції.

def pascal_tri(numRows):
  '''Виводить трикутник Паскаля з numRows рядками.'''
  for i in range(numRows):
    # цикл для додавання пробілів
    for j in range(numRows-i+1):
      print(end=" ")

    # цикл для отримання елементів рядка i
    for j in range(i+1):
      # nCr = n!/((n-r)!*r!)
      print(factorial(i)//(factorial(j)*factorial(i-j)), end=" ")

  # виведення кожного рядка на новий рядок
    print("\n")

Функція працює наступним чином:

Функція pascal_tri має один обов’язковий параметр numRows: кількість рядків.
Загалом є numRows рядків. Для кожного рядка i ми додаємо numRows – i пробілів перед першим елементом рядка.
Потім ми застосовуємо формулу nCr для розрахунку окремих елементів. Для рядка i елементи є iCj, де j = {0,1,2,..,i}.
Використовуємо //, який виконує цілочисельне ділення, оскільки нам потрібні цілі числа.
Після обчислення всіх елементів у рядку, виведіть наступний рядок на новий рядок.

🔗 Оскільки ми додали рядок документації, ви можете використовувати вбудовану функцію help Python або атрибут __doc__ для доступу до рядка документації функції. Наступний фрагмент коду показує, як це зробити.

help(pascal_tri)

# Вивід
Help on function pascal_tri in module __main__:

pascal_tri(numRows)
    Виводить трикутник Паскаля з numRows рядками.

pascal_tri.__doc__

# Вивід
Виводить трикутник Паскаля з numRows рядками.

Тепер викличемо функцію з кількістю рядків як аргумент.

pascal_tri(3)

# Вивід
     1
    1 1
   1 2 1

Перші 3 рядки трикутника Паскаля виведені, як і очікувалось.

Виведення трикутника Паскаля за допомогою рекурсії

У попередньому розділі ми визначили математичний вираз для кожного елемента трикутника Паскаля. Однак ми не скористалися зв’язком між елементами у двох послідовних рядках.

Фактично, ми використовували попередній рядок для обчислення елементів наступного рядка. Чи можемо ми скористатися цим і розробити рекурсивну реалізацію функції pascal_tri?

Так, давайте зробимо це!

У рекурсивній реалізації функція повторно викликає сама себе, поки не досягне базового випадку. У побудові трикутника Паскаля ми починаємо з першого рядка з одним елементом 1, а потім створюємо наступні рядки.

Отже, виклик функції pascal_tri(numRows) у свою чергу викликає pascal_tri(numRows-1) і так далі, доки не досягне базового випадку pascal_tri(1).

Розглянемо приклад, де потрібно вивести перші 3 рядки трикутника Паскаля. На наступному зображенні пояснюється, як рекурсивні виклики відправляються у стек і як рекурсивні виклики функції повертають рядки трикутника Паскаля.

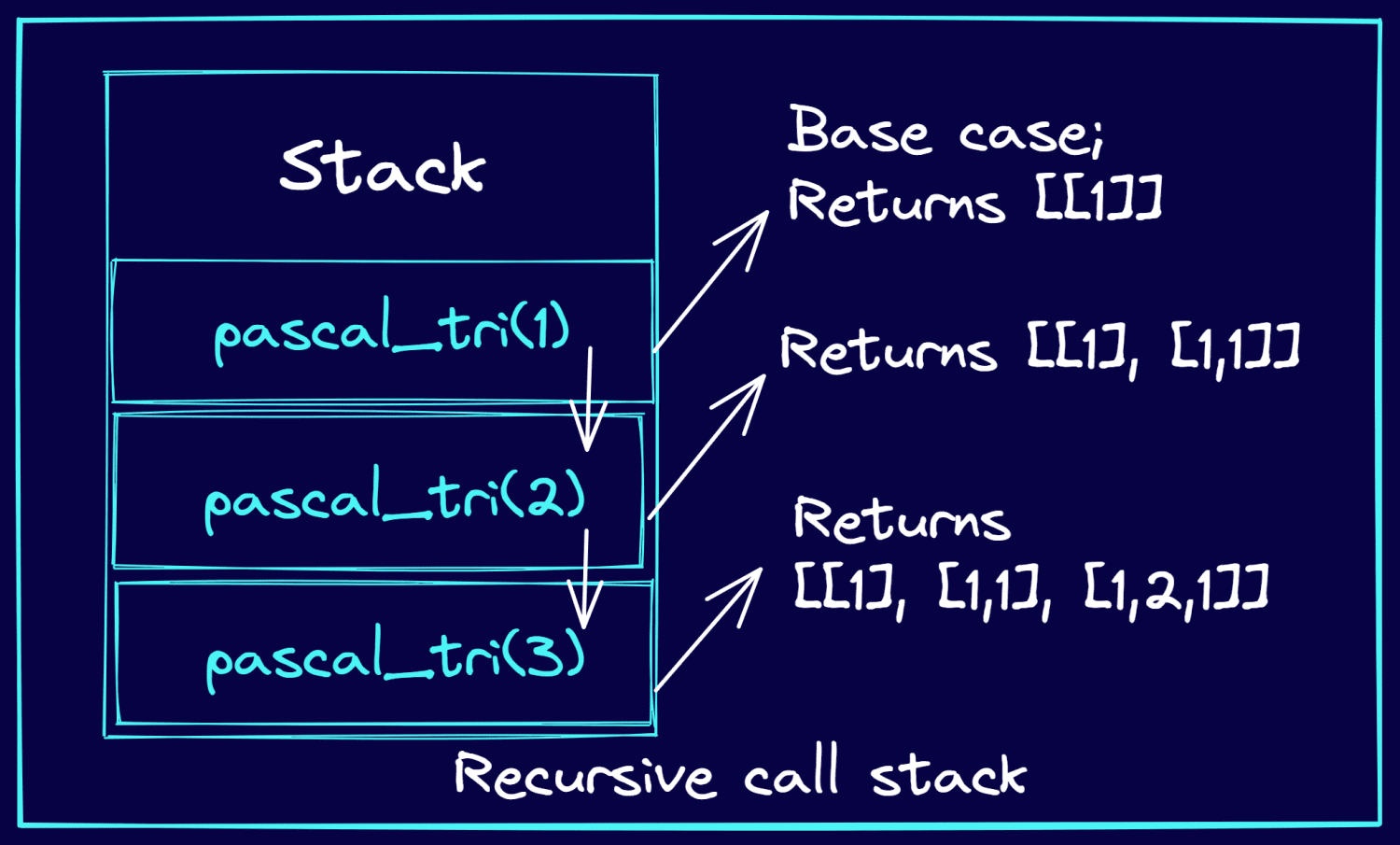
▶️ Запустіть наступний код, щоб рекурсивно згенерувати рядки трикутника Паскаля.

def pascal_tri(numRows):
    '''Виводить трикутник Паскаля з numRows рядками.'''
    if numRows == 1:
        return [[1]] # базовий випадок досягнуто!
    else:
        res_arr = pascal_tri(numRows-1) # рекурсивний виклик pascal_tri
        # використовувати попередній рядок для обчислення поточного рядка
        cur_row = [1] # кожен рядок починається з 1
        prev_row = res_arr[-1]
        for i in range(len(prev_row)-1):
            # сума 2 елементів безпосередньо зверху
            cur_row.append(prev_row[i] + prev_row[i+1])
        cur_row += [1] # кожен рядок закінчується на 1
        res_arr.append(cur_row)
        return res_arr

Ось декілька важливих моментів:

Ми використовували вкладений список як структуру даних, де кожен рядок трикутника Паскаля сам є списком, наприклад: [[рядок 1], [рядок 2],…,[рядок n]].
Виклик функції pascal_tri(numRows) запускає серію рекурсивних викликів з numRows – 1, numRows – 2 аж до 1 як аргументи. Ці виклики надсилаються у стек.
Коли numRows == 1, ми досягаємо базового випадку і функція повертає [[1]].
Отриманий список використовується наступними функціями у стеку викликів для обчислення наступного рядка.
Якщо cur_row – це поточний рядок, то cur_row[i] = попередній_рядок[i] + попередній_рядок[i+1] — сума 2 елементів безпосередньо над поточним індексом.

Оскільки повернений масив є вкладеним списком (списком списків), потрібно налаштувати пробіли і вивести елементи, як показано в коді нижче.

tri_array = pascal_tri(5)

for i,row in enumerate(tri_array):
  for j in range(len(tri_array) - i + 1):
    print(end=" ") # пробіли на початку
  for j in row:
    print(j, end=" ") # вивести елементи
  print("\n")  # вивести новий рядок

Результат виводиться правильно, як показано нижче!

Python-функція для виведення трикутника Паскаля для numRows ≤ 5

Обидва методи, про які ми дізналися, працюють для виведення трикутника Паскаля для будь-якої кількості рядків numRows.

Однак бувають ситуації, коли потрібно вивести трикутник Паскаля для меншої кількості рядків. Якщо кількість рядків, які потрібно вивести, не перевищує 5, ви можете скористатися простим методом.

Подивіться на ілюстрацію нижче. І ви побачите, що степені числа 11 ідентичні елементам трикутника Паскаля. Зауважте, що це працює лише до 4-го степеня числа 11. Тобто 11 у степені {0, 1, 2, 3, 4} дає елементи у рядках з 1 до 5 трикутника Паскаля.

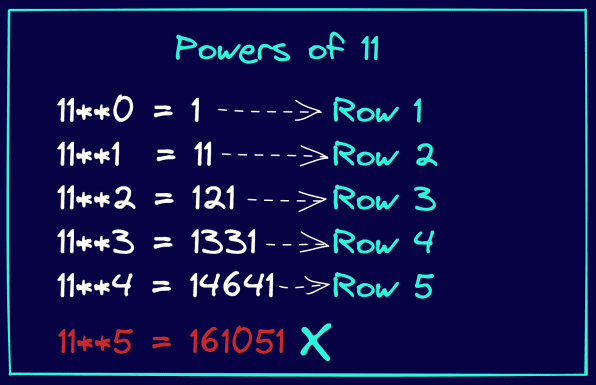
Давайте перепишемо визначення функції, як показано нижче:

def pascal_tri(numRows):
  '''Виводить трикутник Паскаля з numRows рядками.'''
  for i in range(numRows):
    print(' '*(numRows-i), end='')
    # обчислити степінь 11
    print(' '.join(str(11**i)))

Ось як працює функція pascal_tri:

Як і в попередніх прикладах, ми налаштовуємо пробіли.
Потім ми використовуємо оператор піднесення до степеня Python (**), щоб обчислити степені числа 11.
Оскільки степені 11 за замовчуванням є цілими числами, перетворюємо їх на рядок за допомогою str(). Тепер ви маєте степінь 11 у вигляді рядків.
Рядки у Python є ітерованими, тому ви можете переглядати їх і отримувати доступ до символів по одному.
Далі можна використовувати метод join() з синтаксисом: <роздільник>.join(<ітерований об’єкт>), щоб об’єднати елементи в <ітерований об’єкт>, використовуючи <роздільник> як роздільник.
Тут вам потрібен один пробіл між символами, тому <роздільник> буде ‘ ‘, а <ітерований об’єкт> — рядок: степінь 11.

Перевіримо, чи функція працює належним чином.

pascal_tri(5)

# Вивід
     1
    1 1
   1 2 1
  1 3 3 1
 1 4 6 4 1

Як інший приклад, викличемо функцію pascal_tri з 4 як аргумент.

pascal_tri(4)

# Вивід
     1
    1 1
   1 2 1
  1 3 3 1

Сподіваємось, тепер ви розумієте, як легко можна виводити трикутник Паскаля для numRows у діапазоні від 1 до 5.

Висновок

Ось, що ми вивчили:

Як побудувати трикутник Паскаля із заданою кількістю рядків. Кожне число у рядку є сумою двох чисел безпосередньо над ним.
Розробили Python-функцію за формулою nCr = n!/(nr)!.r! для обчислення елементів трикутника Паскаля.
Після цього вивчили рекурсивну реалізацію функції.
Наостанок, ми вивчили найоптимальніший метод побудови трикутника Паскаля для numRows до 5 — використовуючи степені 11.

Якщо ви хочете покращити свої навички Python, навчіться множити матриці, перевіряти, чи є число простим, а також розв’язувати задачі з операціями над рядками. Бажаємо вдалого програмування!