У цьому посібнику ви дізнаєтеся, як створити програму на Python для визначення, чи є задане число простим.
Можливо, ви стикалися з математичними задачами на перевірку простоти чисел під час проходження тестів з програмування. Зараз ви навчитеся розробляти ефективний спосіб вирішення цієї проблеми.
У цьому навчальному матеріалі ви:
- освіжите свої знання про прості числа,
- напишете код на Python, який перевіряє, чи є число простим, і
- оптимізуєте його для досягнення алгоритмічної складності O(√n).
Розпочнімо наше дослідження.
Що ж таке просте число?
Спершу розглянемо визначення простих чисел.
У теорії чисел, натуральне число n вважається простим, якщо воно має рівно два дільники: 1 та саме число (n). Згадаємо зі шкільної програми: число i називається дільником числа n, якщо n ділиться на i без залишку. ✅
У таблиці нижче наведено кілька чисел, їхні дільники та зазначено, чи є вони простими.
| n | Дільники | Просте число? |
| 1 | 1 | Ні |
| 2 | 1, 2 | Так |
| 3 | 1, 3 | Так |
| 4 | 1, 2, 4 | Ні |
| 7 | 1, 7 | Так |
| 15 | 1, 3, 5, 15 | Ні |
З таблиці вище ми можемо зробити висновки:
- 2 – найменше просте число.
- 1 є дільником будь-якого числа.
- Кожне число n є дільником самого себе.
Таким чином, 1 та n є тривіальними дільниками будь-якого числа n. Просте число не повинно мати жодних інших дільників, крім цих двох.
Це означає, що при перевірці чисел від 2 до n – 1, не має бути жодного нетривіального дільника, який би ділив n без залишку.
O(n) Алгоритм для перевірки простоти числа в Python
У цьому розділі ми формалізуємо описаний вище підхід у вигляді функції Python.
Ми можемо перебрати всі числа від 2 до n – 1, використовуючи об’єкт `range()` у Python.
У Python функція `range(початок, кінець, крок)` повертає об’єкт діапазону. Далі, можна ітерувати по цьому об’єкту, щоб отримати послідовність чисел від початку до кінця-1 зі заданим кроком.
Оскільки нам потрібна послідовність цілих чисел від 2 до n-1, ми використаємо `range(2, n)` у циклі `for`.
Наш алгоритм буде таким:
- Якщо ми знайдемо число, яке ділить n без залишку, то n не є простим числом.
- Якщо ми перебрали всі числа від 2 до n – 1 і не знайшли жодного дільника, то число n є простим.
Функція Python для перевірки простоти числа
Використовуючи вищезазначене, ми можемо визначити функцію `is_prime()`:
def is_prime(n):
for i in range(2,n):
if (n%i) == 0:
return False
return True
Тепер розглянемо визначення цієї функції.
- Функція `is_prime()` приймає натуральне число n як аргумент.
- Якщо в заданому діапазоні (2, n-1) знайдено дільник, то функція повертає `False`, оскільки число не є простим.
- Якщо ж цикл пройде повністю без знаходження дільника, функція поверне `True`.
Викличемо функцію з різними аргументами та перевіримо результати.
is_prime(2)
# True
is_prime(8)
# False
is_prime(9)
# False
is_prime(11)
# True
Як бачимо, 2 та 11 є простими числами (функція повертає `True`), а 8 і 9 – ні (функція повертає `False`).
Оптимізація функції `is_prime()` на Python
Можлива невелика оптимізація. Зверніть увагу на перелік дільників у таблиці.
| Число | Дільники |
| 6 | 1, 2, 3, 6 |
| 10 | 1, 2, 5, 10 |
| 18 | 1, 2, 3, 6, 9, 18 |
Єдиний дільник n, який є більшим за n/2 – це саме n.
Отже, немає потреби перебирати числа до n – 1. Достатньо перевірити лише числа до n/2.
Якщо до n/2 не знайдено нетривіального дільника, то його не буде і після n/2.
Змінимо функцію `is_prime()`, щоб перевіряти дільники в діапазоні (2, n/2):
def is_prime(n):
for i in range(2,int(n/2)):
if (n%i) == 0:
return False
return True
Перевіримо результат, викликавши функцію:
is_prime(9)
# False
is_prime(11)
# True
Хоча здається, що ми провели оптимізацію, цей алгоритм не є ефективнішим з точки зору складності виконання. Обидва алгоритми мають O(n) часову складність: вона пропорційна до значення n, тобто лінійна.
Чи можна досягнути кращого результату? Так, це можливо!
▶️ Перейдіть до наступного розділу, щоб дізнатися, як покращити часову складність перевірки простих чисел.
O(√n) Алгоритм перевірки простоти числа на Python
Дільники числа завжди зустрічаються парами.
Якщо a є дільником числа n, то існує такий дільник b, що a * b = n.
Розглянемо приклад.
У таблиці нижче наведено дільники числа 18, які зустрічаються парами. Ви можете перевірити це для інших чисел.
Зауважте, що √18 ≈ 4.24.
У парах дільників (a, b), якщо a < 4.24, то b > 4.24 – наприклад, (2, 9) та (3, 6).
Дільники числа 18 у вигляді пар.
Якщо n є повним квадратом, то a = b = √n є одним із дільників.
▶️ Подивіться на дільники 36 у таблиці. Оскільки 36 є повним квадратом, a = b = 6 є одним із дільників. Для інших пар дільників (a, b) справедливо a < 6 та b > 6.
Дільники числа 36 у вигляді пар.
Підсумовуючи, маємо:
- Будь-яке число n можна записати як n = a * b.
- Якщо n є повним квадратом, то a = b = √n.
- Якщо a < b, то a < √n та b > √n.
- Інакше, якщо a > b, то a > √n та b < √n.
Отже, замість перебору чисел до n/2, можна обмежитися перевіркою до √n. Це значно ефективніше.
Як змінити функцію `is_prime()` на O(√n)?
Оптимізуємо функцію перевірки простоти числа в Python.
import math
def is_prime(n):
for i in range(2,int(math.sqrt(n))+1):
if (n%i) == 0:
return False
return True
Розглянемо визначення функції:
- Імпортуємо вбудований математичний модуль Python і використовуємо функцію `math.sqrt()` для обчислення квадратного кореня.
- Оскільки n може не бути ідеальним квадратом, перетворимо корінь на ціле число за допомогою `int(var)`.
- Щоб переконатися, що ми справді перевіряємо √n, ми додаємо одиницю, оскільки функція `range()` виключає кінцеву точку.
Перевіримо, чи правильно працює наша функція `is_prime()`:
is_prime(8)
# False
is_prime(15)
# False
is_prime(23)
# True
У наступному розділі ми створимо графіки, щоб наочно порівняти O(n) та O(√n).
Візуальне порівняння O(n) та O(√n)
▶️ Запустіть наведений нижче код у середовищі Jupyter Notebook:
import numpy as np
import seaborn as sns
import pandas as pd
n = 20
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
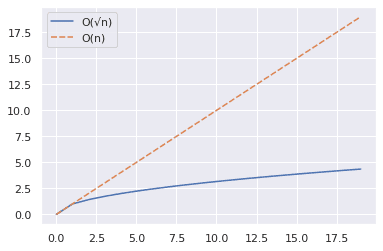
Код створює графіки для n та √n для заданого діапазону значень.
- Функція NumPy `arange()` створює масив чисел.
- Зібрані значення n та √n (до 20, не включаючи) в об’єкт pandas DataFrame.
- Для побудови графіка використовується функція `seaborn.lineplot()`.
З графіка видно, що √n значно менше за n.

Збільшимо діапазон до 2000 і повторимо ці кроки.
import numpy as np
import seaborn as sns
import pandas as pd
n = 2000
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
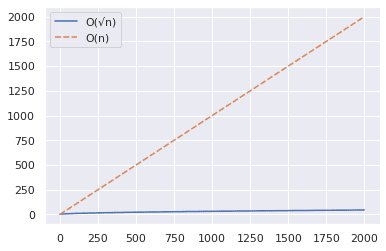
З графіка видно, що алгоритм O(√n) значно швидший для перевірки великих чисел на простоту.
Наприклад, 2377 є простим числом – перевірте це! 😀
Алгоритм O(n) потребує близько 2000 кроків, тоді як O(√n) лише 49. ✅
Висновок
⏳ Підсумуємо основні моменти:
- Для перевірки, чи є число простим, наївний метод передбачає перебір всіх чисел в діапазоні (2, n-1). Якщо не знайдено дільника, то n є простим.
- Оскільки єдиний дільник n, більший за n/2, це n, можна перевіряти лише до n/2.
- Обидва підходи мають часову складність O(n).
- Оскільки дільники зустрічаються парами, можна перебирати лише до √n. Цей алгоритм значно швидший, особливо при перевірці великих чисел.
Сподіваюсь, ви зрозуміли, як перевірити простоту числа в Python. Наступним кроком можете ознайомитись з нашим посібником про операції з рядками в Python, де ви навчитеся перевіряти рядки на паліндром, анаграми тощо.
До зустрічі в наступних посібниках! Бажаємо успішного кодування! 👩🏽💻