Що таке перевірка гіпотез і як вона працює?
Перевірка гіпотез – це потужний інструмент, який використовується аналітиками як у приватному, так і в державному секторах для формулювання обґрунтованих припущень щодо характеристик цільової сукупності на основі аналізу вибіркових даних. Цей метод дозволяє перевірити, наскільки певні припущення відповідають реальності, використовуючи статистичні методи.
Якщо ви коли-небудь працювали з аналізом даних, ви напевно знайомі з перевіркою гіпотез. Це важливий інструмент для підтвердження або спростування припущень про сукупність на основі даних вибірки.
Існує безліч підходів до формулювання припущень, але не всі вони забезпечують однакову точність. Тому, якщо ви маєте сумніви щодо достовірності ваших даних, використання їх без перевірки може бути ризикованим. Перевірка гіпотез є ефективною стратегією для підвищення точності та надійності висновків. Цей інструмент відіграв ключову роль в аналізі даних про населення.
У цій статті ми розглянемо, що таке перевірка гіпотез, як вона працює, її переваги та сфери застосування.
Отже, почнемо!
Визначення перевірки гіпотез
Перевірка гіпотез – це метод статистичного висновування, який застосовується для оцінки достатності даних для підтвердження певної гіпотези про сукупність. Цей метод дозволяє аналітикам оцінити гіпотезу і визначити, наскільки точно припущення відповідає фактичним даним.
Простими словами, це статистичний процес, який дозволяє робити висновки про сукупність на основі аналізу вибіркових даних. Аналітикам часто складно отримати повну інформацію про всю сукупність, але за допомогою перевірки гіпотез можна робити обґрунтовані прогнози та приймати рішення на основі вибіркових даних.
Види гіпотез, що перевіряються
Існує кілька видів гіпотез, які використовуються в процесі перевірки:
- Нульова гіпотеза: Це припущення про відсутність зв’язку або різниці між досліджуваними змінними в вибіркових даних. Вона стверджує, що будь-які відмінності, виявлені у вибірці, є випадковими і не відображають реальну ситуацію в сукупності.
- Альтернативна гіпотеза: Це протилежне нульовій гіпотезі припущення про існування зв’язку або різниці між змінними в даних. Вона є основною рушійною силою у процесі тестування.
- Неспрямована гіпотеза: Ця гіпотеза стверджує, що між змінними існує різниця, але не вказує напрямку цієї різниці. Вона показує, що фактичне значення відрізняється від прогнозованого, але не каже, є воно більшим чи меншим.
- Спрямована гіпотеза: Ця гіпотеза конкретно визначає напрямок зв’язку між змінними. Вона передбачає, що одна змінна впливає на іншу в певному напрямку (збільшення або зменшення).
- Статистична гіпотеза: Ця гіпотеза допомагає оцінити, чи дані та значення відповідають певній гіпотезі. Вона особливо корисна для формулювання припущень про результат параметра сукупності на основі вибіркових даних.
Далі розглянемо основні методи перевірки гіпотез.
Основні методи перевірки гіпотез
Для того, щоб оцінити достовірність гіпотези, аналітикам потрібні переконливі докази, що ґрунтуються на аналізі вибіркових даних. Процес тестування зазвичай починається зі встановлення нульової та альтернативної гіпотез.
Перевірка гіпотез використовує різні методи для оцінки вибіркових даних. Вибір конкретного методу залежить від характеристик даних та розміру вибірки.
Тест на нормальність
Цей метод використовується для оцінки, чи вибіркові дані мають нормальний розподіл. Під час тестування перевіряється, чи точки даних згруповані навколо середнього значення, утворюючи дзвоноподібну криву.
Z-тест
Z-тест застосовується, коли дані мають нормальний розподіл і потрібно перевірити, чи відрізняються середні значення двох сукупностей, якщо відома дисперсія даних. Цей метод часто використовується, коли розмір вибірки перевищує 30 одиниць. Центральна гранична теорема є ще однією підставою для використання Z-тесту, оскільки вона стверджує, що зі збільшенням розміру вибірки, вибірковий розподіл наближається до нормального.
T-тест
T-тест використовується, коли розмір вибірки обмежений (менше 30) і стандартне відхилення параметра невідоме. Він застосовується для обчислення довірчих інтервалів для даних про сукупність.
Хі-квадрат
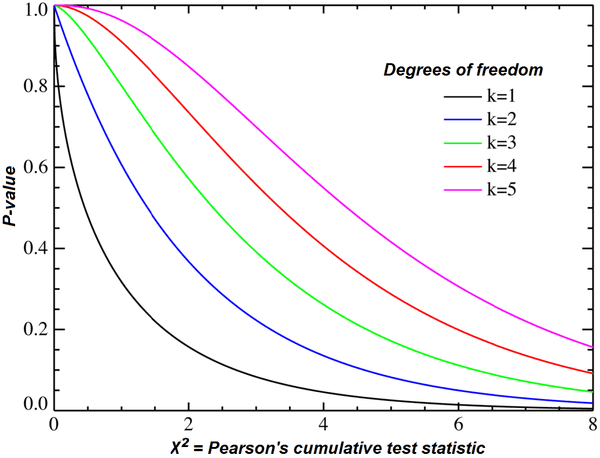
Тест хі-квадрат є популярним методом для оцінки узгодженості даних з розподілом, що очікується. Його часто застосовують, коли необхідно перевірити дисперсію генеральної сукупності. Існує кілька варіантів тесту хі-квадрат, серед яких найпоширенішими є тести дисперсії та незалежності.
ANOVA
Дисперсійний аналіз (ANOVA) використовується для порівняння середніх значень двох або більше груп даних. Цей метод аналізує залежність між залежною та незалежною змінними. ANOVA є розширенням Z-тестів та T-тестів, дозволяючи порівнювати більше двох груп.

Процес перевірки гіпотез
Аналітики використовують вибіркові дані для аналізу та вимірювання в процесі перевірки гіпотез. Під час тестування дані вибірки використовуються для перевірки нульової та альтернативної гіпотез.
Як було зазначено раніше, нульова та альтернативна гіпотези є взаємовиключними, і в процесі тестування лише одна з них може бути вірною. Проте, іноді нульову гіпотезу може бути відхилено, навіть якщо альтернативна гіпотеза не завжди є правильною.
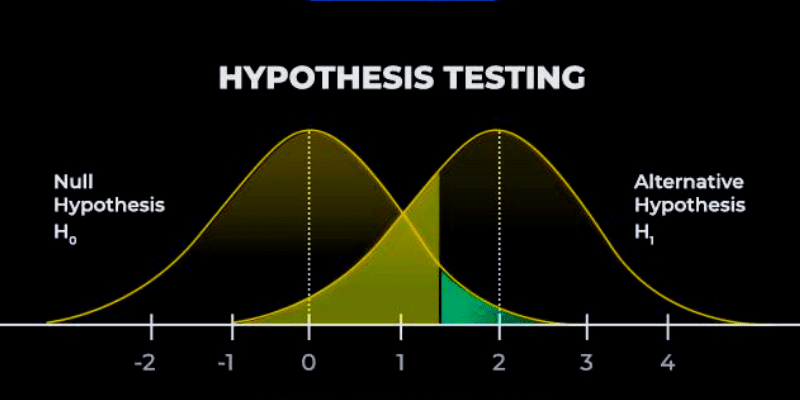
p-значення: Це значення показує ймовірність отримання результатів, настільки ж або більш екстремальних, ніж ті, що були отримані, якщо нульова гіпотеза є правильною. Значення p порівнюється з рівнем значущості (альфа-рівнем), який встановлюється заздалегідь.
Рівень значущості визначає прийнятний рівень ризику відхилення нульової гіпотези, коли вона насправді є вірною. Важливо пам’ятати, що результат перевірки гіпотези може призвести до двох типів помилок:
- Помилка першого типу (Тип I): відбувається, коли нульову гіпотезу відхиляють, хоча вона насправді є правильною.
- Помилка другого типу (Тип II): відбувається, коли нульову гіпотезу приймають, хоча вона насправді є хибною.
Усі значення, які призводять до відхилення нульової гіпотези, зберігаються в критичній області, яка відокремлює критичні регіони від інших.
Етапи перевірки гіпотез
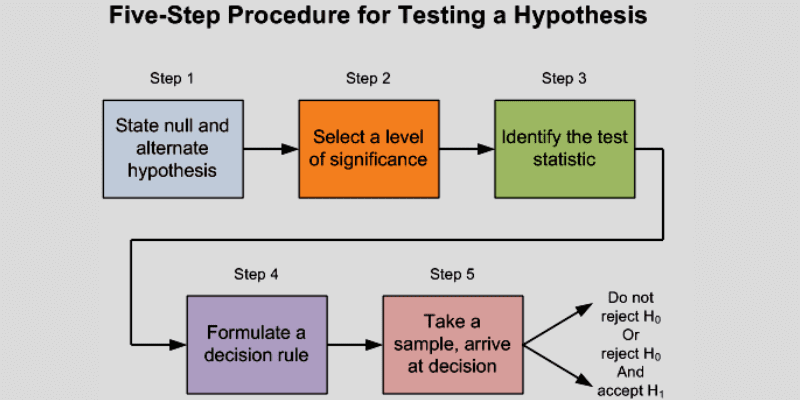
Перевірка гіпотез зазвичай включає такі кроки:
- Формулювання гіпотез: На цьому етапі аналітик визначає нульову та альтернативну гіпотези, які є взаємовиключними. Наприклад, нульова гіпотеза може стверджувати про відсутність різниці в середньому ІМТ, а альтернативна – про наявність значної різниці.
- Планування: На цьому етапі розробляється план аналізу вибіркових даних. Здійснюється збір вибіркових даних, які мають відповідати гіпотезі.
- Аналіз вибіркових даних: На цьому етапі відбувається аналіз вибіркових даних для перевірки на їх надмірність. Важливо переконатися, що вибірки є незалежними та достатньо великими.
- Обчислення тестової статистики: На цьому етапі обчислюється тестова статистика та значення p. Значення p визначається на основі припущення, що нульова гіпотеза вірна.
- Оцінка результату: На останньому етапі оцінюється результат перевірки гіпотези. Приймається рішення, чи відхиляти нульову гіпотезу, чи заявити про її ймовірність на основі аналізу вибіркових даних.
Далі розглянемо переваги перевірки гіпотез.
Переваги перевірки гіпотез
Переваги перевірки гіпотез:
- Допомагає оцінити обґрунтованість висновків щодо даних.
- Створює надійну основу для прийняття рішень на основі вибіркових даних.
- Дозволяє визначити статистичну значущість вибіркових даних.
- Підвищує надійність та валідність результатів тестування в будь-якому систематичному процесі.
Також метод дозволяє узагальнити висновки, отримані на основі вибіркових даних, на більшу сукупність залежно від необхідності.
Застосування перевірки гіпотез
Перевірка гіпотез широко використовується в різних секторах для оцінки точності вибіркових даних. Ось кілька прикладів реального застосування:
#1. Клінічні випробування
Перевірка гіпотез використовується для визначення ефективності нових лікарських засобів або методів лікування на основі вибіркових даних. Наприклад, лікар може перевірити, чи знижує новий препарат рівень калію у пацієнтів. Лікар вимірює рівень калію у групі пацієнтів до початку лікування та після його застосування.

Далі лікар проводить перевірку гіпотези, де H0: Uпісля = Uперед, означає, що рівень калію після лікування не змінився. Альтернативна гіпотеза Ha: Uпісля < Uперед вказує на зниження рівня калію після лікування. Якщо значення p менше рівня значущості, лікар робить висновок про ефективність лікування.
#2. Виробництво
На виробничих підприємствах перевірка гіпотез допомагає оцінити ефективність нових методів виробництва. Наприклад, виробники можуть використовувати перевірку гіпотез, щоб визначити, чи зменшує новий метод кількість бракованої продукції.

Припустимо, що кількість бракованих виробів становить 300 на партію. Виробник визначає середню кількість бракованої продукції до та після застосування нового методу. Проводиться перевірка гіпотез з гіпотезами H0: Uпісля = Uперед (кількість браку не змінилася) та HA: Uпісля ≠ Uперед (кількість браку змінилася). Якщо значення p менше рівня значущості, робиться висновок про зміну кількості бракованої продукції.
#3. Сільське господарство
У сільському господарстві перевірка гіпотез використовується для оцінки впливу добрив та пестицидів на ріст рослин. Біологи можуть перевірити, чи стимулює нове добриво ріст рослин більше ніж на 15 дюймів. Біолог застосовує добриво протягом місяця, щоб зібрати вибіркові дані.

При перевірці гіпотези H0 U = 15 дюймів показує, що добриво не впливає на ріст, тоді як HA: U > 15 дюймів вказує на збільшення росту. Якщо p-значення менше рівня значущості, біолог робить висновок про те, що добриво сприяє більшому росту рослин.
Ресурси для навчання
#1. Статистика: покроковий вступ від Udemy

Цей курс від Udemy надає крок за кроком вступ до статистики, включаючи перевірку гіпотез, довірчі інтервали та інше. Курс містить практичні приклади та уроки.
#2. Основна статистика для аналізу даних Udemy
Цей курс Udemy охоплює основи статистики, використовуючи реальні приклади та проекти. Він включає теми, як перевірка гіпотез, розподіл ймовірностей та регресійний аналіз.
#3. Статистика для науки про дані та бізнес-аналізу

Цей курс Udemy призначений для фахівців з аналізу даних та бізнес-аналітиків. Він охоплює різні статистичні теми, включаючи перевірку гіпотез, інференційну та описову статистику та регресійний аналіз.
#4. Перевірка гіпотези Джима Фроста
Ця книга є практичним посібником з перевірки гіпотез, допомагаючи аналітикам приймати рішення на основі даних. У ній розглядаються такі теми, як довірчі інтервали, p-значення, рівні значущості та багато іншого.
#5. Перевірка гіпотези Скотта Хартсхорна
Ця книга призначена для початківців, які шукають стислий вступ до перевірки гіпотез. Вона пояснює значення статистичних даних, їх типи та роботу без необхідності глибоких знань статистики.
Висновок
Перевірка гіпотез є важливим інструментом для перевірки припущень та розробки обґрунтованих висновків. Вона використовується в різних секторах, включаючи виробництво, сільське господарство, клінічні випробування та ІТ. Перевірка гіпотез є точним методом для прийняття рішень на основі даних. Для отримання глибших знань у цій галузі, рекомендується переглянути наведені вище навчальні ресурси.