Сортування є однією з найбільш затребуваних операцій у сфері програмування. Ефективність сортування безпосередньо залежить від обраного алгоритму, і неправильний вибір може призвести до значних затримок у виконанні.
У цій статті ми розглянемо різноманітні підходи до сортування, проаналізувавши їхні особливості та сфери застосування.
Ми детально розглянемо різні алгоритми сортування, надаючи на кожному етапі їхньої реалізації. Для наочності деякі приклади будуть представлені мовою Python. Однак, розуміючи принцип роботи алгоритму, ви зможете легко адаптувати його до будь-якої іншої мови програмування. Адже, по суті, це лише питання синтаксису.
Цей посібник проведе вас від найменш ефективних до найпотужніших методів сортування. Не хвилюйтеся, якщо на початку щось здаватиметься складним. Просто слідуйте інструкціям і практикуйте, втілюючи вивчене в життя.
Отже, давайте поринемо у світ алгоритмів сортування!
Сортування вставками
Сортування вставками – це один із найпростіших для розуміння алгоритмів сортування. Його відносна легкість у реалізації робить його привабливим для невеликих масивів даних. Однак, варто зазначити, що його продуктивність помітно знижується при обробці великих обсягів інформації, через що він не є оптимальним вибором у таких випадках.
Принцип сортування вставками полягає у підтримці двох частин масиву: відсортованої та невідсортованої.
На початковому етапі відсортована підмножина містить лише перший елемент масиву. Потім, з невідсортованої частини послідовно вибираються елементи, які вставляються на відповідні позиції у відсортованій підмножині.
Щоб краще зрозуміти, як це працює, давайте розглянемо покрокову візуалізацію сортування вставкою на конкретному прикладі.
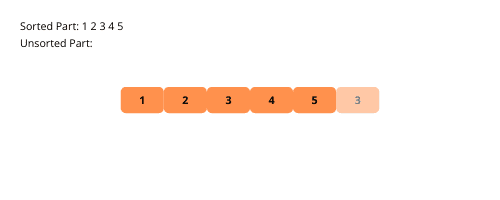
Розглянемо покрокову реалізацію сортування вставкою:
- Спочатку створюємо масив із довільними числовими значеннями.
- Починаємо ітерацію по масиву з другого елемента.
- Зберігаємо поточну позицію та значення елемента у відповідних змінних.
- Організовуємо цикл, який продовжується до тих пір, поки не дійдемо до початку масиву або поки не знайдемо елемент, менший за поточний.
- Зміщуємо елементи масиву на одну позицію вправо.
- Зменшуємо поточну позицію на одиницю.
- Коли цикл закінчиться (або досягнуто початку масиву, або знайдено менший елемент), вставляємо поточний елемент на звільнену позицію.
Часова складність сортування вставками становить O(n^2), а просторова – O(1).
Отже, масив відсортовано. Нижче наведено приклад коду. Сподіваюся, у вас встановлено Python. Якщо ні, ознайомтеся з інструкцією по встановленню. Також, ви можете скористатися онлайн-компілятором Python.
def insertion_sort(arr, n):
for i in range(1, n):
# зберігаємо поточну позицію та елемент
current_position = i
current_element = arr[i]
# ітеруємо до тих пір, поки
# не досягнемо першого елемента або
# поточний елемент менший за попередній
while current_position > 0 and current_element < arr[current_position - 1]:
# оновлюємо поточний елемент попереднім
arr[current_position] = arr[current_position - 1]
# переходимо до попередньої позиції
current_position -= 1
# оновлюємо елемент на поточній позиції
arr[current_position] = current_element
if __name__ == '__main__':
# ініціалізація масиву
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
insertion_sort(arr, 9)
# виводимо масив
print(str(arr))
Сортування вибором
Сортування вибором має схожий принцип із сортуванням вставками, але з певною відмінністю. Цей алгоритм також поділяє масив на відсортовану та невідсортовану частини. На кожній ітерації ми знаходимо мінімальний елемент у невідсортованій частині та ставимо його на останню позицію відсортованої частини.
Для кращого розуміння розглянемо візуальну ілюстрацію процесу сортування вибором.
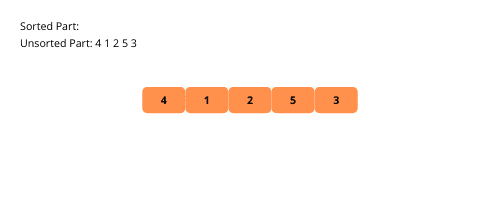
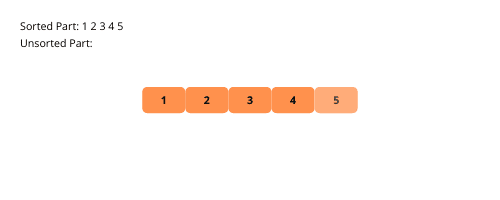
Давайте розглянемо кроки реалізації сортування вибором.
- Створюємо масив із набором довільних числових даних.
- Здійснюємо ітерацію по масиву.
- Записуємо індекс мінімального елемента.
- Організовуємо цикл, який ітерує від поточного елемента до останнього.
- Перевіряємо, чи поточний елемент менший за мінімальний.
- Якщо так, то перезаписуємо індекс мінімального елемента.
- Змінюємо місцями поточний елемент із мінімальним, використовуючи їх індекси.
Часова складність сортування вибором дорівнює O(n^2), а просторова – O(1).
Спробуйте реалізувати цей алгоритм самостійно, адже він схожий на сортування вставкою. Нижче ви знайдете приклад коду для перевірки.
def selection_sort(arr, n):
for i in range(n):
# зберігаємо індекс мінімального елемента
min_element_index = i
for j in range(i + 1, n):
# перевіряємо та оновлюємо індекс мінімального елемента
if arr[j] < arr[min_element_index]:
min_element_index = j
# міняємо місцями поточний елемент з мінімальним
arr[i], arr[min_element_index] = arr[min_element_index], arr[i]
if __name__ == '__main__':
# ініціалізація масиву
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
selection_sort(arr, 9)
# виводимо масив
print(str(arr))
Бульбашкове сортування
Бульбашкове сортування – ще один простий алгоритм сортування. Він полягає у багаторазовому порівнянні та перестановці сусідніх елементів, доки весь масив не стане відсортованим.
Алгоритм проходить масивом і переміщує поточний елемент на наступну позицію, якщо він більший за наступний елемент.
Ілюстрації нижче наочно демонструють принцип роботи бульбашкового сортування.
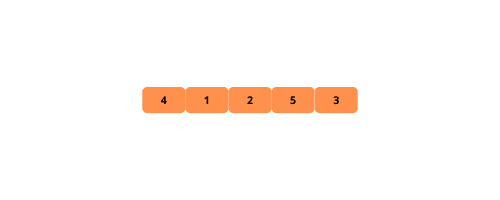
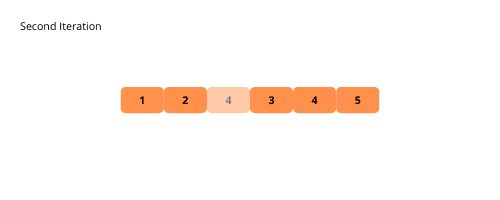
Розглянемо кроки реалізації бульбашкового сортування.
Часова складність бульбашкового сортування становить O(n^2), а просторова – O(1).
Тепер ви легко зможете реалізувати бульбашкове сортування. Нижче наведено приклад коду.
def bubble_sort(arr, n):
for i in range(n):
# ітеруємо від 0 до n-i-1, оскільки останні i елементів вже відсортовані
for j in range(n - i - 1):
# перевіряємо наступний елемент
if arr[j] > arr[j + 1]:
# міняємо місцями сусідні елементи
arr[j], arr[j + 1] = arr[j + 1], arr[j]
if __name__ == '__main__':
# ініціалізація масиву
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
bubble_sort(arr, 9)
# виводимо масив
print(str(arr))
Сортування злиттям
Сортування злиттям – це рекурсивний алгоритм сортування, який є ефективнішим за попередні алгоритми з точки зору часової складності. В основі його роботи лежить принцип “розділяй і володарюй”.
Алгоритм поділяє масив на дві половини, які потім сортуються окремо. Після цього відсортовані половини об’єднуються в один відсортований масив.
Оскільки це рекурсивний алгоритм, масив ділиться до тих пір, поки не досягне найпростішого випадку (масив з одним елементом).
Настав час розглянути ілюстрації.
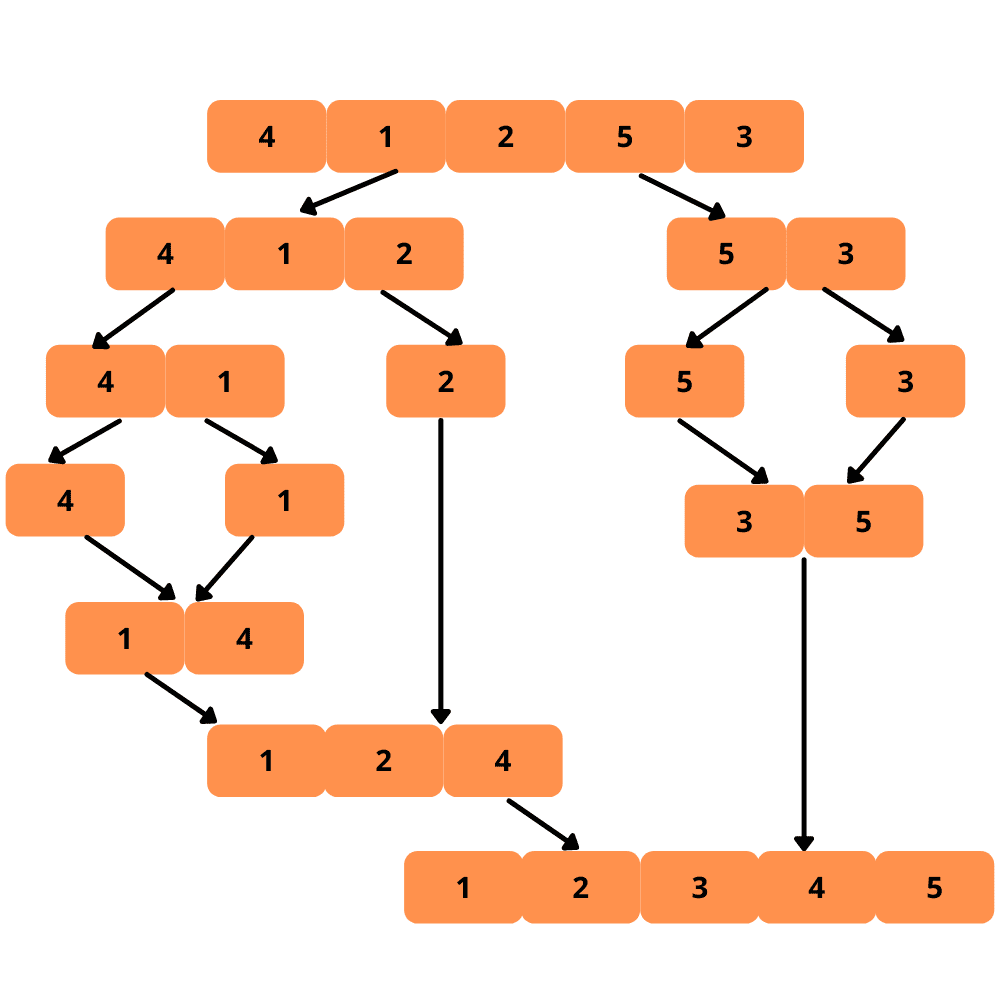
Розглянемо кроки реалізації сортування злиттям.
- Ініціалізуємо масив довільними числовими даними.
- Створюємо функцію merge для об’єднання підмасивів у відсортований масив. Функція приймає масив, а також лівий, середній та правий індекси.
- Визначаємо довжини лівого і правого підмасивів за допомогою заданих індексів.
- Копіюємо елементи масиву у відповідні лівий та правий підмасиви.
- Ітеруємо по обох підмасивах.
- Порівнюємо елементи підмасивів.
- Замінюємо елемент масиву на менший елемент з двох підмасивів.
- Перевіряємо наявність елементів, що залишилися в будь-якому підмасиві.
- Додаємо залишки в масив.
- Створюємо функцію merge_sort із параметрами: масивом, лівим та правим індексами.
- Якщо лівий індекс більший або дорівнює правому, то функція повертається.
- Знаходимо середню точку масиву, щоб поділити його на дві половини.
- Рекурсивно викликаємо merge_sort з відповідними лівими, правими та середніми індексами.
- Після рекурсивних викликів об’єднуємо масиви з допомогою функції злиття.
Часова складність сортування злиттям дорівнює O(n log n), а просторова – O(1).
Ось і все, що стосується реалізації сортування злиттям. Перегляньте код нижче.
def merge(arr, left_index, mid_index, right_index):
# лівий та правий масиви
left_array = arr[left_index:mid_index+1]
right_array = arr[mid_index+1:right_index+1]
# визначаємо довжини лівого та правого масивів
left_array_length = mid_index - left_index + 1
right_array_length = right_index - mid_index
# індекси для об'єднання двох масивів
i = j = 0
# індекс для заміни елементів масиву
k = left_index
# ітеруємо по двох підмасивах
while i < left_array_length and j < right_array_length:
# порівнюємо елементи лівого та правого масивів
if left_array[i] < right_array[j]:
arr[k] = left_array[i]
i += 1
else:
arr[k] = right_array[j]
j += 1
k += 1
# додаємо залишки з лівого та правого масивів
while i < left_array_length:
arr[k] = left_array[i]
i += 1
k += 1
while j < right_array_length:
j += 1
k += 1
def merge_sort(arr, left_index, right_index):
# базовий випадок рекурсивної функції
if left_index >= right_index:
return
# знаходимо середній індекс
mid_index = (left_index + right_index) // 2
# рекурсивні виклики
merge_sort(arr, left_index, mid_index)
merge_sort(arr, mid_index + 1, right_index)
# об'єднуємо два підмасиви
merge(arr, left_index, mid_index, right_index)
if __name__ == '__main__':
# ініціалізація масиву
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
merge_sort(arr, 0, 8)
# виводимо масив
print(str(arr))
Висновок
Існує багато інших алгоритмів сортування, але ми розглянули лише деякі з найбільш поширених. Сподіваюсь, вам було цікаво дізнатись більше про сортування.
Наступним кроком буде вивчення алгоритмів пошуку.
Успіхів у програмуванні! 🙂 👨💻