З моменту зародження ідеї квантового комп’ютера у 1980 році, сфера квантових обчислень зазнала значного розвитку, особливо протягом останнього десятиліття. Велика кількість компаній активно працює над розробкою квантових комп’ютерів.
Розуміння концепції квантових обчислень може бути складним завданням для більшості з нас, а великий обсяг доступної інформації часто не розкриває важливих деталей.
Ця стаття має на меті роз’яснити цю тему. Після її прочитання ви отримаєте вичерпне уявлення про те, що таке квантові обчислення, їх різні типи, принципи роботи, алгоритми, моделі, підходи, виклики та застосування.
Що собою являють квантові комп’ютери?
Квантові комп’ютери використовують відмінний від звичних нам класичних комп’ютерів підхід до розв’язання задач. Квантові комп’ютери мають ряд переваг у порівнянні зі звичайними для певних типів завдань. Ці переваги обумовлені їхньою здатністю перебувати у великій кількості станів одночасно, на відміну від класичних комп’ютерів, які можуть перебувати лише в одному стані за раз.
 Джерело зображення: IBM
Джерело зображення: IBM
Для розуміння принципів роботи квантових комп’ютерів, необхідно розібратися з трьома ключовими поняттями: суперпозицією, заплутаністю та інтерференцією.
Основою звичайного комп’ютера є біти, тоді як в квантовому комп’ютері використовуються квантові біти, або кубіти. Вони працюють за різними принципами.
Класичний біт можна порівняти з перемикачем, що приймає значення 0 або 1, які представляють двійкову інформацію. При вимірюванні біта ми фіксуємо його поточний стан, але з кубітами все по-іншому. Кубіт є більш складною системою.
Суперпозиція
Для наочності можна уявити кубіт як стрілку, що вказує в 3D-просторі. Якщо вона спрямована вгору, кубіт перебуває в стані 1, а якщо вниз – у стані 0, подібно до класичного біта. Однак кубіт також може перебувати в стані суперпозиції, коли стрілка спрямована в будь-якому іншому напрямку.
Стан суперпозиції є комбінацією станів 0 і 1.
 Стан суперпозиції
Стан суперпозиції
При вимірюванні кубіта, результат буде або 1, або 0. Ймовірність отримання того чи іншого значення залежить від напрямку стрілки.
Якщо стрілка спрямована більше вгору, ймовірність отримати 1 вища, ніж 0. Якщо стрілка спрямована вниз, то ймовірність отримати 0 вища. Якщо вона розташована точно на екваторі, то ймовірність отримати кожен зі станів становить 50%.
Таким чином, ми розглянули ефект суперпозиції. Тепер перейдемо до заплутаності.
Обплутаність
У класичних комп’ютерах біти абсолютно незалежні один від одного. Стан одного біта не впливає на стан жодного іншого. Однак у квантових комп’ютерах кубіти можуть бути заплутані, тобто їхні стани стають взаємозалежними і формують єдиний квантовий стан.
Розглянемо два кубіти, кожен з яких перебуває у власному стані суперпозиції, але ще не є заплутаним. Ймовірності для кожного кубіта є незалежними.
При заплутуванні кубітів незалежні ймовірності відкидаються. Замість цього обчислюється розподіл ймовірностей усіх можливих комбінацій станів (00, 01, 10 або 11).

Ключовим є те, що заплутані кубіти є взаємозалежними. Зміна напрямку стрілки одного кубіта змінює розподіл ймовірностей для всієї системи. Кубіти більше не є незалежними, а стають частиною одного великого стану.
Це справедливо незалежно від кількості кубітів. Зверніть увагу, що для одного кубіта розподіл ймовірностей припадає на 2 стани.
Для двох кубітів розподіл ймовірностей розповсюджується між чотирма станами. Для трьох кубітів маємо розподіл на 8 станів. Кількість станів подвоюється з кожним доданим кубітом.
Отже, квантовий комп’ютер з n кубітами може перебувати в комбінації 2^n станів. Це є ключовою відмінністю між класичними і квантовими комп’ютерами.

Класичні комп’ютери можуть перебувати в будь-якому потрібному стані, але тільки в одному одночасно, в той час як квантові комп’ютери можуть перебувати в суперпозиції всіх цих станів одночасно.
Може виникнути запитання, як перебування в такому стані суперпозиції може бути корисним для обчислень. Для відповіді на це питання необхідно розглянути останній компонент: інтерференцію.
Інтерференція
Щоб пояснити ефект інтерференції, звернімося до зображення кубіта, що технічно називається сферою Блоха. Фактичний стан кубіта є більш абстрактним поняттям, яке описується квантовою хвильовою функцією.
Хвильові функції є фундаментальним математичним описом всіх елементів в квантовій механіці.
Коли багато кубітів об’єднано разом, їхні хвильові функції складаються у загальну хвильову функцію, що описує стан квантового комп’ютера.
Складання хвильових функцій є процесом інтерференції. Так само, як і у випадку з хвилями на воді, при додаванні хвиль вони можуть конструктивно накладатися і підсилювати одна одну, або деструктивно взаємодіяти і гасити одна одну.
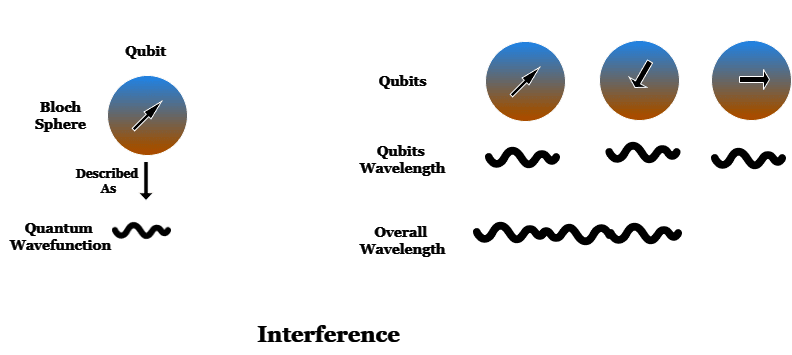
Загальна хвильова функція квантового комп’ютера визначає ймовірності різних станів. Змінюючи стани кубітів, можна змінити ймовірність виявлення різних станів при вимірюванні квантового комп’ютера.
Пам’ятайте, що квантовий комп’ютер може перебувати в суперпозиції мільйонів станів одночасно, але при вимірюванні ми отримуємо тільки один з них.
При розв’язанні обчислювальної задачі на квантовому комп’ютері, необхідно використовувати конструктивну інтерференцію для підвищення ймовірності отримання правильної відповіді, і деструктивну для зменшення ймовірності отримання неправильних відповідей. Завдяки цьому, при вимірюванні буде отримано правильну відповідь.
Квантові алгоритми
Спосіб реалізації цього процесу є сферою квантових алгоритмів. Мотивацією для розробки квантових обчислень є те, що теоретично існує ряд задач, які можна розв’язати на квантовому комп’ютері, але неможливо на класичних.
Розглянемо їх. Існує велика кількість квантових алгоритмів. В цій статті ми зосередимося на найвідомішому та історично важливому – алгоритмі Шора.
#1. Алгоритм Шора
Якщо дано два великих числа і потрібно знайти їхній добуток, існує швидкий і ефективний класичний алгоритм для розв’язання цієї задачі. Однак, якщо відомий добуток, і потрібно знайти вихідні числа, то це завдання є значно складнішим.
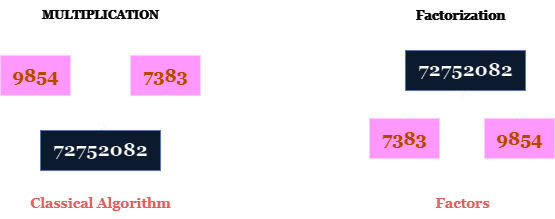
Це завдання відоме як факторизація. Числа, з яких отримано добуток, називають факторами. Складність їхнього знаходження полягає у величезному просторі пошуку. Не існує ефективного класичного алгоритму для знаходження множників великих чисел.
З цієї причини ми використовуємо цю математичну особливість для шифрування даних в Інтернеті: для захисту веб-сайтів, електронних листів та банківських рахунків. Якщо відомі фактори, то інформацію легко розшифрувати. Але якщо фактори невідомі, то спочатку їх потрібно знайти. Це завдання є надзвичайно складним навіть для найпотужніших комп’ютерів.
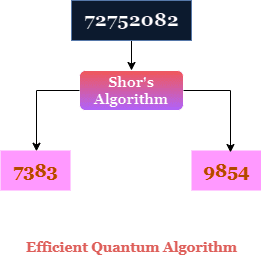 Алгоритм Шора
Алгоритм Шора
Саме тому в 1994 році, коли Пітер Шор опублікував швидкий квантовий алгоритм для ефективного знаходження множників великих цілих чисел, це викликало значний резонанс.
В цей момент багато людей почали серйозно розглядати ідею квантових обчислень, оскільки з’явився перший реальний приклад застосування, що має величезні наслідки для безпеки у реальному світі.
Коли ми говоримо про “швидкий” квантовий алгоритм, наскільки він є швидким, і наскільки швидшим він є порівняно з класичним комп’ютером? Для відповіді на ці запитання необхідно розглянути теорію квантової складності.
Квантова теорія складності
Квантова теорія складності є підгалуззю загальної теорії обчислювальної складності, яка займається класифікацією алгоритмів. Алгоритми розподіляють на групи в залежності від того, наскільки ефективно вони працюють на комп’ютерах.
Класифікація визначається рівнем зростання складності розв’язання задачі в міру збільшення її розміру. Класичні комп’ютери легко розв’язують задачі в межах прямокутника P, а будь-яка задача поза ним означає відсутність ефективних класичних алгоритмів. Факторизація великих чисел належить саме до таких задач.
Існує область BQP, де квантові комп’ютери працюють ефективно, а класичні – ні. Саме такі задачі квантові комп’ютери зможуть розв’язувати краще, ніж класичні.
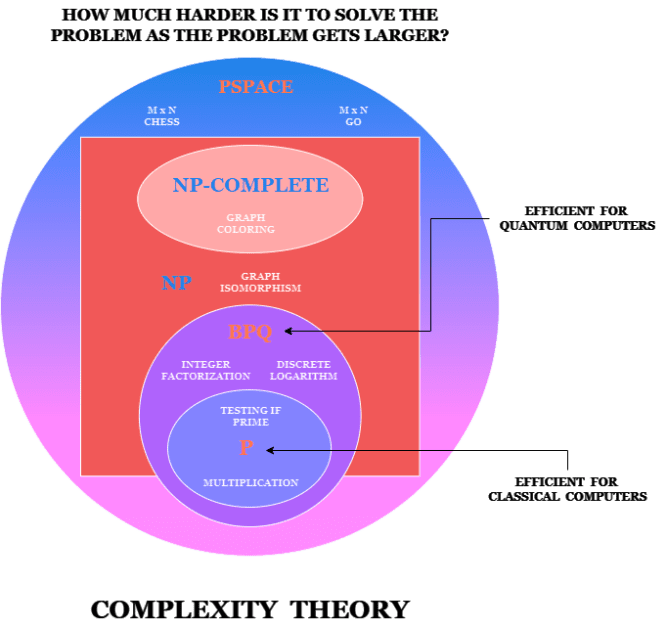
Теорія складності досліджує, наскільки важко розв’язати задачу при її збільшенні. Якщо, наприклад, спочатку є число з 8 цифр, потім додається ще одна цифра, наскільки важче буде розкласти нове число на множники? Чи вдвічі важче? Чи експоненціально складніше? Якою є ця тенденція при додаванні все більшої кількості цифр? Це називається складністю або масштабуванням, і для факторизації воно є експоненціальним.
Будь-яка задача, в якій N є показником степеня, є експоненціально складною. Ці експоненціальні задачі є надзвичайно складними, і в інформатиці можна отримати визнання, якщо знайти кращий алгоритм для їх розв’язання.
Одним з прикладів є алгоритм Шора, який використовує можливості квантових комп’ютерів для створення алгоритму, що розв’язує факторизацію чисел зі значно кращим масштабуванням, ніж найкращий класичний алгоритм.
Найкращий класичний алгоритм є експоненціальним, тоді як алгоритм Шора – поліноміальним. Це є надзвичайно важливим досягненням у світі теорії складності, оскільки це перетворює нерозв’язну задачу на розв’язну.
Розв’язання можливе за наявності робочого квантового комп’ютера, над створенням якого зараз працюють вчені. Проте, поки що не варто турбуватися про безпеку банківського рахунку, оскільки сучасні квантові комп’ютери не здатні виконувати алгоритм Шора для великих чисел.

IBM Quantum
Для цього знадобиться велика кількість кубітів. Найсучасніші універсальні квантові комп’ютери мають близько 433 кубіти.
Крім того, розробляються постквантові схеми шифрування, які не використовують факторизацію цілих чисел. Також в цьому може допомогти квантова криптографія.
Отже, це був огляд одного з квантових алгоритмів, але їх існує набагато більше, і кожен має різний рівень прискорення.
#2. Алгоритм Гровера
Іншим яскравим прикладом є алгоритм Гровера, який може здійснювати пошук у неструктурованих списках даних швидше, ніж найкращий класичний алгоритм.
Слід з обережністю ставитися до невірного уявлення про можливості класичних комп’ютерів. Це дуже універсальні пристрої, і немає гарантії, що хтось не винайде ефективний класичний алгоритм для розв’язання таких складних проблем, як факторизація цілих чисел.
Хоча це є малоймовірним, але не виключається. Крім того, є задачі, які неможливо розв’язати на класичних комп’ютерах (наприклад, проблема зупинки). І їх також неможливо розв’язати на квантовому комп’ютері.
Отже, з точки зору обчислень класичні і квантові комп’ютери еквівалентні. Відмінності полягають в алгоритмах, які вони можуть виконувати. Квантовий комп’ютер можна симулювати на класичному і навпаки.
Симуляція квантового комп’ютера на класичному стає експоненціально складнішою з кожним доданим кубітом.
Причина полягає в тому, що класичним комп’ютерам складно моделювати квантові системи. Квантові комп’ютери, будучи квантовими системами, не мають цієї проблеми. Це підводить нас до улюбленого застосування квантових комп’ютерів: квантового моделювання.
#3. Квантова симуляція
Квантова симуляція використовує комп’ютер для моделювання таких речей, як хімічні реакції або поведінка електронів у різних матеріалах. Квантові комп’ютери також мають експоненційне прискорення в цій області, оскільки класичним комп’ютерам важко імітувати квантові системи.
Моделювання квантових систем з невеликою кількістю частинок є важким завданням навіть для найпотужніших суперкомп’ютерів. Хоча ми ще не можемо цього зробити на квантових комп’ютерах, основна мета їхнього розвитку – моделювання все більших і більших квантових систем.
Це включає такі галузі, як поведінка екзотичних матеріалів при низьких температурах, розуміння надпровідності, або вивчення хімічних реакцій для підвищення їх ефективності. Одним з прикладів є виробництво добрив з мінімальними викидами вуглекислого газу, оскільки їх виробництво відповідає за близько 2% глобальних викидів вуглецю.
Детальніше про моделювання квантової хімії.

Квантова симуляція
Інші потенційні застосування квантового моделювання включають вдосконалення сонячних панелей, акумуляторів, розробку нових ліків, хімікатів або матеріалів для аерокосмічної галузі.
Квантове моделювання дозволить швидко створювати прототипи різних матеріалів на квантовому комп’ютері і перевіряти всі їхні фізичні параметри замість фізичного створення і тестування в лабораторії, що є більш ресурсозатратним і дорогим процесом.
Це може значно прискорити процеси та зменшити час і витрати. Слід зазначити, що це лише потенційні застосування, оскільки поки що немає квантових комп’ютерів, що можуть розв’язувати реальні задачі краще за звичайні. Однак, квантові комп’ютери добре підходять для розв’язання саме таких задач.
Моделі квантових комп’ютерів

В галузі квантових комп’ютерів існує велика різноманітність підходів до перетворення різних типів квантових систем на квантові комп’ютери. Розглянемо два рівня нюансів.
Модель схеми
В схемній моделі, кубіти працюють разом, і спеціальні логічні вентилі впливають на декілька кубітів одночасно, змінюючи їхній стан без вимірювання. Ці вентилі розміщені в певному порядку, створюючи квантовий алгоритм. Наприкінці процесу кубіти вимірюють для отримання результату.
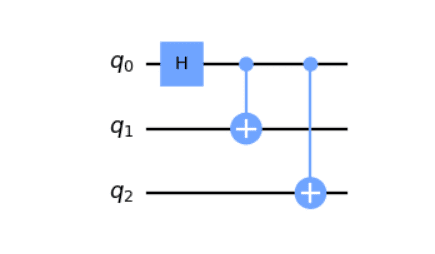 Автор зображення: qskit
Автор зображення: qskit
Адіабатичні квантові обчислення
В адіабатичних квантових обчисленнях використовують той факт, що кожна фізична система завжди прагне перейти в стан мінімальної енергії. Задачу формують таким чином, щоб найнижчий енергетичний стан квантової системи відповідав розв’язку задачі.
Квантовий відпал
Квантовий відпал не є універсальною моделлю квантових обчислень, але працює за аналогічним принципом, що і адіабатичні обчислення. Система шукає мінімальний енергетичний стан енергетичного ландшафту.
Топологічні квантові обчислення
В цьому підході кубіти створюють з так званої майоранівської квазічастинки нульового режиму. Передбачається, що ці квазічастинки є більш стабільними через їхню фізичну відокремленість.
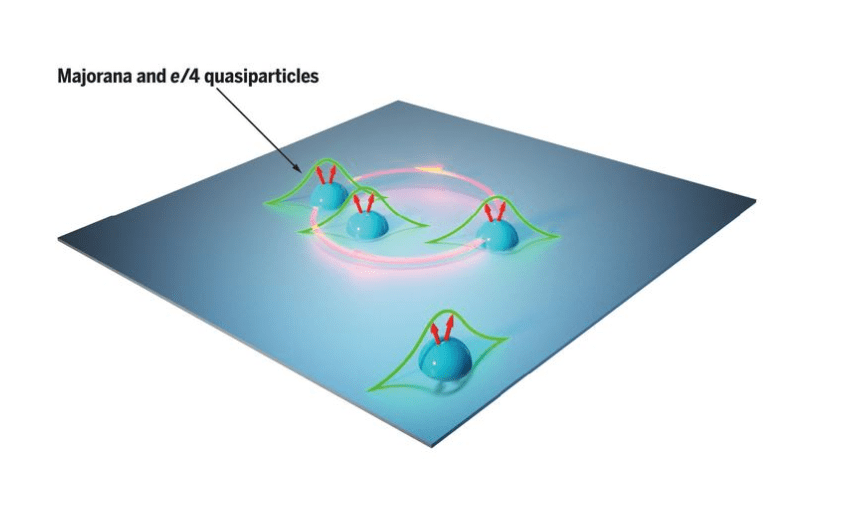 Автор зображення: Civilsdaily
Автор зображення: Civilsdaily
Проблеми в розробці
Незалежно від обраного підходу, усі стикаються зі схожим набором перешкод.
- Декогеренція: Керування квантовими системами є дуже складним завданням, оскільки взаємодія із зовнішнім світом призводить до втрати інформації. Це називається декогеренцією. Кубіти створюються з фізичних матеріалів, і для їх контролю та вимірювання необхідні інші матеріали. Кубіти схильні до взаємодії з усім. Тому потрібен дуже ретельний дизайн кубітів для захисту від взаємодії з навколишнім середовищем.
- Шум: Необхідно захищати кубіти від будь-яких видів шуму, таких як космічне випромінювання, радіація, теплова енергія або випадкові частинки. Певна кількість декогеренції і шуму є неминучою в будь-якій фізичній системі і не може бути повністю усунена.
- Масштабованість: Для кожного кубіта потрібна велика кількість проводів для його маніпуляції та вимірювання. Зі збільшенням кількості кубітів необхідна інфраструктура зростає лінійно, що створює значні інженерні складності. Будь-яка конструкція квантового комп’ютера повинна ефективно заплутувати, контролювати та вимірювати всі кубіти під час масштабування.
- Квантова корекція помилок: Квантова корекція помилок є схемою для створення відмовостійких квантових комп’ютерів за допомогою великої кількості заплутаних кубітів, які представляють один безшумний кубіт. Це вимагає великої кількості фізичних кубітів для створення одного відмовостійкого кубіта.
Фізичні реалізації

Існує велика кількість різноманітних фізичних реалізацій квантових комп’ютерів, оскільки існує багато різних квантових систем, які потенційно можуть бути використані для їх створення. Ось декілька найбільш поширених підходів:
- Надпровідні квантові комп’ютери: Надпровідні кубіти є наразі найпоширенішим підходом. Ці кубіти виготовлені з надпровідних провідників з розривом в надпровіднику, який називається джозефсонівським переходом. Найпопулярніший тип надпровідних кубітів називається трансмон.
- Квантові комп’ютери з квантовою точкою: Кубіти складаються з електронів або груп електронів. Дворівнева система кодується в спіні або заряді електронів. Ці кубіти створюються з напівпровідників, таких як кремній.
- Лінійні оптичні квантові обчислення: Оптичні квантові комп’ютери використовують фотони світла як кубіти та працюють з ними за допомогою оптичних елементів, таких як дзеркала, хвильові пластини та інтерферометри.
- Квантові комп’ютери із захопленими іонами: Заряджені атоми використовуються як кубіти. Ці атоми йонізуються, втрачаючи електрон. Дворівневий стан, який кодує кубіт – це конкретні рівні енергії атома, якими можна маніпулювати за допомогою мікрохвиль або лазерних променів.
- Квантові комп’ютери з кольоровим центром або азотними вакансіями: Кубіти створені з атомів, вбудованих в такі матеріали, як азот в алмазі або карбіді кремнію. Вони використовують спіни ядер вбудованих атомів і заплутуються разом з електронами.
- Нейтральні атоми в оптичних гратках: Цей підхід захоплює нейтральні атоми в оптичну решітку, що є перехресним розташуванням лазерних променів. Дворівневою системою для кубітів може бути надтонкий енергетичний рівень атома або збуджені стани.
Це декілька основних підходів до створення квантових комп’ютерів, кожен з яких має свої унікальні характеристики та проблеми. Квантові обчислення швидко розвиваються, і вибір правильного підходу є важливим для майбутнього успіху.
Застосування квантових комп’ютерів

- Квантова симуляція: Квантові комп’ютери мають потенціал для моделювання складних квантових систем, що дає можливість вивчати хімічні реакції, поведінку електронів у матеріалах та різні фізичні параметри. Це має застосування для вдосконалення сонячних панелей, акумуляторів, розробки ліків, аерокосмічних матеріалів та іншого.
- Квантові алгоритми: Такі алгоритми, як алгоритм Шора та алгоритм Гровера, можуть розв’язувати задачі, що вважаються нерозв’язними для класичних комп’ютерів. Вони мають застосування в криптографії, оптимізації складних систем, машинному навчанні та ШІ.
- Кібербезпека: Квантові комп’ютери становлять загрозу для класичних систем шифрування. Однак, вони також можуть сприяти кібербезпеці шляхом розробки квантово-стійких схем шифрування. Квантова криптографія, галузь, пов’язана з квантовими обчисленнями, може підвищити безпеку.
- Проблеми оптимізації: Квантові комп’ютери можуть розв’язувати складні задачі оптимізації ефективніше, ніж класичні комп’ютери. Це має застосування в різних галузях, від управління ланцюгом поставок до фінансового моделювання.
- Прогнозування погоди та зміна клімату: Хоча в статті немає повної інформації, квантові комп’ютери потенційно можуть покращити моделі прогнозування погоди та допомогти вирішити проблеми, пов’язані зі зміною клімату. Це сфера, яка може отримати користь від квантових обчислень у майбутньому.
- Квантова криптографія: Квантова криптографія підвищує безпеку даних за допомогою квантових принципів безпечного зв’язку. У час зростання кіберзагроз це є дуже важливим.
Необхідно обережно ставитися до потенціалу ажіотажу, оскільки багато заяв про користь квантових комп’ютерів надходять від людей, які активно збирають кошти на їхню розробку.
Історія показує, що люди часто не можуть передбачити, як саме використовуватимуться нові технології. Наприклад, люди, що винайшли перші комп’ютери, не могли уявити Інтернет і все, що з ним пов’язано. Імовірно, те саме буде і з квантовими комп’ютерами.
Заключні думки
Квантові комп’ютери стають кращими з кожним днем. Хоча їх ще не можна використовувати у повсякденному житті, вони мають потенціал для практичного застосування у майбутньому.
В цій статті було розглянуто різні аспекти квантових комп’ютерів, включаючи фундаментальні поняття, такі як суперпозиція, заплутаність та інтерференція.
Далі було досліджено квантові алгоритми, включаючи алгоритм Шора та алгоритм Гровера. Також розглянуто теорію квантової складності та різні моделі квантових комп’ютерів.
В кінці статті були розглянуті виклики, пов’язані з практичним застосуванням квантових обчислень. На завершення було досліджено широкий спектр потенційних застосувань квантових комп’ютерів.
Також можна ознайомитись з поширеними питаннями щодо квантових обчислень.